医療工学解説－論理回路・変調・AD変換

国家試験で出題される論理回路・変調・AD変換について解説します！特に論理回路はよく出題されるので対策は必須！

※スマホから閲覧している場合，数式と表をスクロールできます。

各見出しの重要度は，過去の臨床検査技師国家試験（第52回～最新回まで）の出題率や覚えやすさなどを考慮して主観で表記しています。国家試験を受ける学生以外の方は無視してかまいません。

論理回路（重要度：★★★★★）

論理回路とは？　

ペンギンくん

論理回路って何？

論理演算を行う回路のことだよ。

おるてぃ

ペンギンくん

ろ，論理演算……？

論理演算は，コンピュータが行う演算で，例えば，2つの入力が1のときに1を出力するといった具合だよ。

おるてぃ

ペンギンくん

う～ん，よくわからないなぁ。

とりあえず各論理回路の入力と出力の関係を覚えておけば国家試験は余裕だよ！頑張って！

おるてぃ

論理回路は，コンピュータに使われている重要な回路です。
例えば，この入力とこの入力がされたときに，この出力をするといった感じで使われています。

論理回路は6種類あります。

1. NOT回路（否定回路）
   
2. OR回路（論理和回路）
   
3. AND回路（論理積回路）
   
4. NOR回路（否定論理和回路）
   
5. NAND回路（否定論理積回路）
   
6. XOR回路（排他的論理和回路）
   

ペンギンくん

お，多いね……。本当に覚えること多いね。

ノンノン。病理とかと比べると優しいほうだよ。この6個の形と出力を覚えておけばいいだけなんだから。これで音を上げるようだと合格できないよ？(笑)

おるてぃ

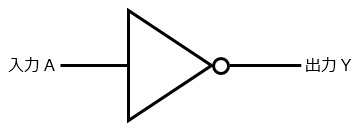
NOT回路（否定回路）　

NOT回路は，入力の逆を出力する回路です。
入力が1（真）なら0（偽）を，0なら1を出力します。
後述する回路と違って，入力は1つです。
回路にある「○」がnotを表しています。

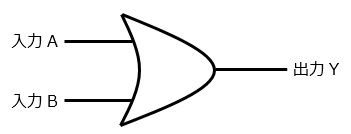
OR回路（論理和回路）　

OR回路は，入力が少なくとも1つ以上1（真）のとき1を出力する回路です。入力が全て0（偽）なら0を出力します。

1個でも1があればOK！1が出力されるよ。

おるてぃ

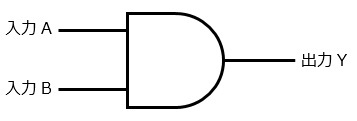
AND回路（論理積回路）　

AND回路は，入力が全て1（真）のときのみ1を出力する回路です。入力に1つでも0（偽）があると0を出力します。

OR回路とAND回路を混同しないために，AND回路の回路記号は「ANDのD」と覚えておきましょう。（混同すると大変なので）

全部1でないと1が出力されないよ。

おるてぃ

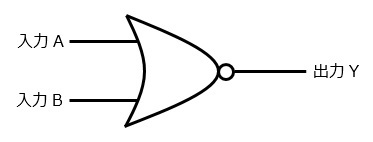
NOR回路（否定論理和回路）　

NORはNOT＋ORのことで，OR回路にNOTを表す○が付いたものです。
OR回路の出力が逆になるだけですので，OR回路を知っておけば覚えてなくとも簡単に書き出せます。

OR回路さえ覚えておけば簡単！

おるてぃ

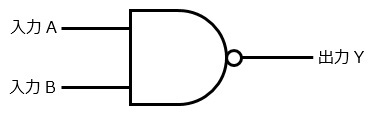
NAND回路（否定論理積回路）　

NANDはNOT＋ANDのことで，AND回路にNOTを表す○が付いたものです。
NOR回路同様，NAND回路はANDの出力が逆になるだけですので，AND回路を知っておけば覚えてなくとも簡単に書き出せます。

AND回路さえ覚えておけばこちらも簡単！

おるてぃ

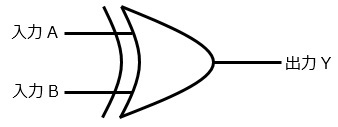
XOR回路（EOR回路，EX-OR回路，排他的論理和回路）　

この回路はちょっと変わった回路で，入力が等しいときに0を，入力が異なるときに1を出力する回路です。
※入力数が3つ以上のときは，入力の1の数が奇数個のときに1を，偶数個のときに0を出力します。

この回路だけはちょっと覚えづらいけど頑張って覚えよう！

おるてぃ

論理回路まとめ　

回路図と入出力の関係は必ず覚えておこう！

おるてぃ

変調（重要度：★★☆☆☆）

変調とは？　

変調とは，データを伝送しやすくするために信号の振幅や周波数を変えることを言います。
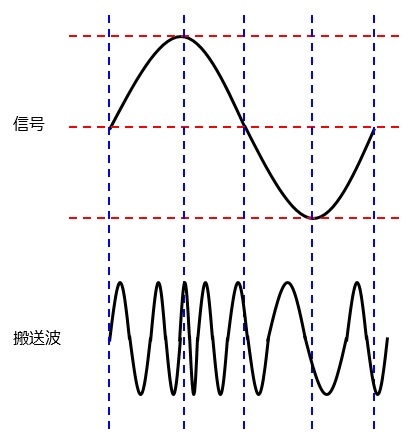
例えば，振幅変調であれば，信号を波の振幅に変えることになります。

ペンギンくん

振幅変調だと，信号の高い部分で振幅が大きくなって，信号の低い部分で振幅が小さくなるってこと？

そうそう，そういうこと。最初はとっつきにくいかもしれないけど，変調方法自体は名称の通りだから，慣れれば意外とわかりやすいかも。

おるてぃ

変調には主に以下の3種類があります。

1. アナログ変調
   
   • 振幅変調（AM）
   • 周波数変調（FM）
2. デジタル変調
   
   • 振幅偏移変調（ASK）
   • 周波数偏移変調（FSK）
   • 位相偏移変調（PSK）
3. パルス変調
   
   • パルス振幅変調（PAM）
   • パルス周波数変調（PFM）
   • パルス幅変調（PWM）
   • パルス位置変調（PPM）
   • パルス数変調（PNM）
   • パルス符号変調（PCM）

アナログ変調　

信号がアナログ（連続）であるものを変調する方法です。変調された搬送波も連続波となります。

振幅変調（AM：amplitude modulation）

信号を搬送波の振幅の大小で伝送する方法です。
雑音（ノイズ）による振幅の変化の影響を受けるため，雑音に弱いという欠点があります。

周波数変調（FM：frequency modulation）

信号を搬送波の周波数の高低で伝送する方法です。

デジタル変調　

信号がデジタル（不連続）であるものを変調する方法です。

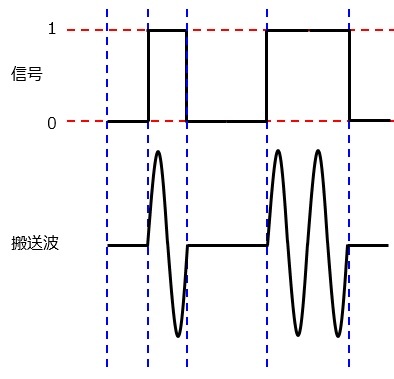
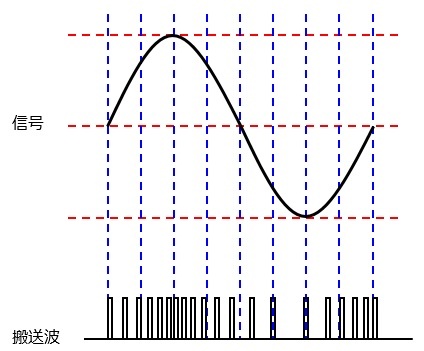
振幅偏移変調（ASK：amplitude shift keying）

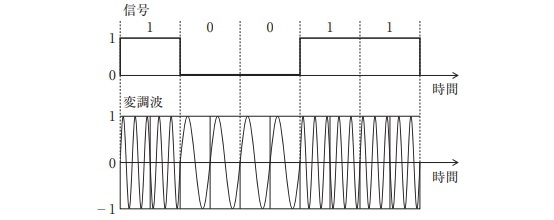
信号を搬送波の振幅の大小（0なら小・1なら大）で伝送する方法です。
アナログ変調との違いは，振幅の変化が2種類しかないことです。
AM同様，雑音（ノイズ）による振幅の変化の影響を受けるため，雑音に弱いという欠点があります。

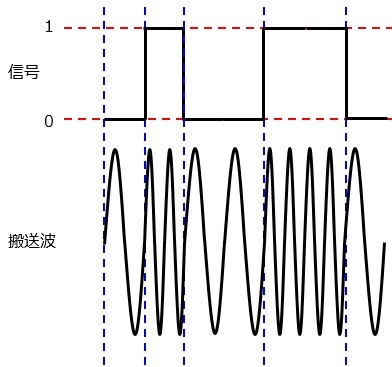
周波数偏移変調（FSK：frequecy shift keying）

信号を搬送波の周波数の高低（0なら低・1なら高）で伝送する方法です。
アナログ変調との違いは，周波数の変化が2種類しかないことです。

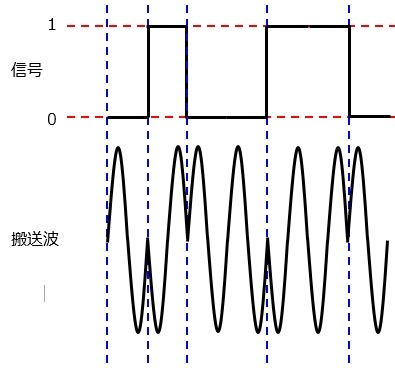
位相偏移変調（PSK︰phase shift keying）

信号を搬送波の位相の変化で伝送する方法です。

位相の変化とは，波が上向きであれば下向きに，下向きであれば上向きにするということです。

パルス変調　

信号（アナログ・デジタル）をパルス波に変調する方法です。

この変調の特徴は，信号を一定周期ごとに分けて考えるということです。（PFMは例外）

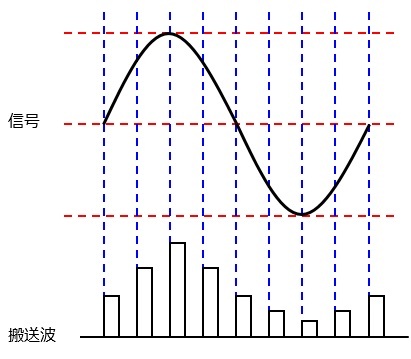
パルス振幅変調（PAM：pulse amplitude modulation）

信号をパルス波の振幅の大小で伝送する方法です。
AM・ASKと同様，雑音（ノイズ）に弱いという欠点があります。

パルス周波数変調（PFM：pulse frequency modulation）

信号をパルス波の周波数の高低で伝送する方法です。
パルス数変調（PNM）と似ていますが，違いはPNMが一定周期ごと（＝青点線間）のパルス波の数の変化に対し，PFMは各パルス波の間隔を変化させているということです。

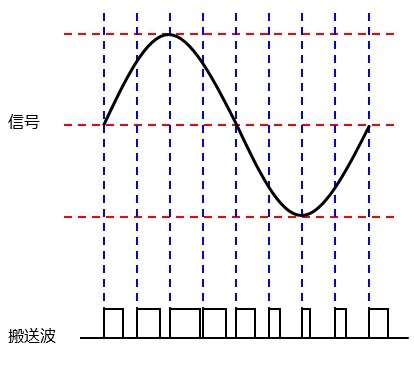
パルス幅変調（PWM：pulse width modulation）

信号をパルス波のデューティ比（パルス波の幅の最大を1としたときの，それぞれのパルス波の幅の割合）の変化で伝送する方法です。

パルス位置変調（PPM：pulse position modulation）

信号をパルス波の位置変化で伝送する方法です。

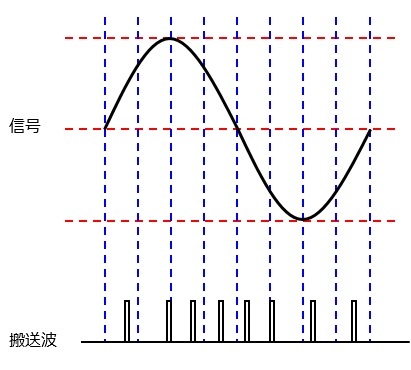
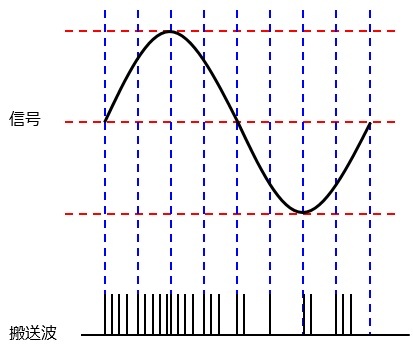
パルス数変調（PNM：pulse number modulation）

信号をパルス波の数の変化で伝送する方法です。

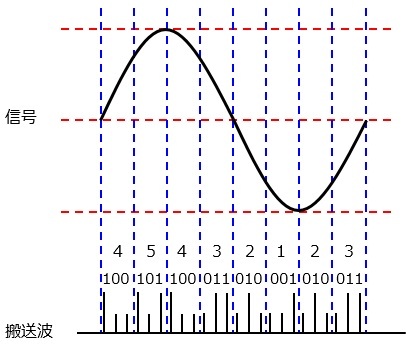
パルス符号変調（PCM：pulse code modulation）

信号を2進数に変換して，そこから2進数に応じたパルス波に変化させて伝送する方法です。

変調まとめ　​​

余裕のある人は変調名と波形を覚えておこう。

おるてぃ

AD変換（重要度：★★★★★）

ペンギンくん

また難しい単語が……。

ぱっと見は難しいかもしれないけど，意外と単純だから大丈夫！

おるてぃ

AD変換とは？　

AD（アナログ・デジタル）変換とは，アナログ信号をデジタル信号に変換させることです。

生体信号はアナログ信号（連続した信号）ですが，これを目に見える形で表現するためには，必ずデジタル信号（0/1で表す信号）に変換する必要があります。（生体計測機器はデジタル信号を扱うため。）

そこでAD変換が必要となってきます。
AD変換では，下に示す3ステップで行います。

1. 標本化（sampling）
2. 量子化（quantization）
3. 符号化（encode）

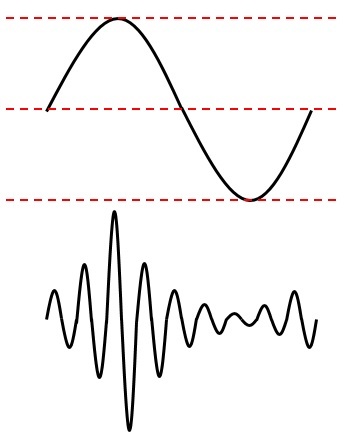
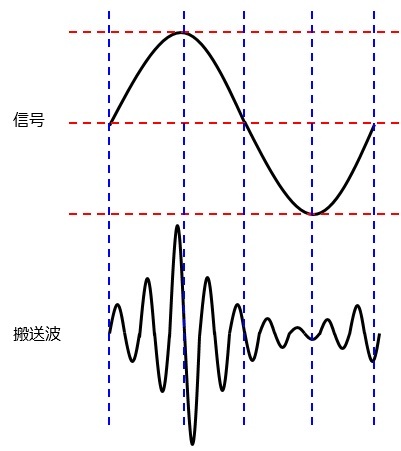
標本化（sampling）　

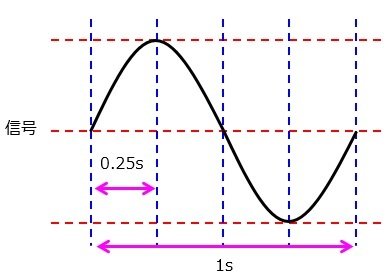
アナログ信号を一定時間ごとに区切り，それぞれの信号の値を読み込む段階です。
標本化するときのアナログ信号を区切る時間をサンプリング周期［s］，サンプリング周期の逆数をサンプリング周波数［Hz］といいます。（サンプリング周波数は，1秒あたりのアナログ信号を何等分に区切るかというのを表しています）

上の図だと，サンプリング周期は0.25s，サンプリング周波数は$\frac{1}{0.25}$＝4Hzとなります。

サンプリング周期が短いほど（＝サンプリング周波数が高いほど），信号を細かく区切るため，アナログ信号を忠実に表現できるようになります。

ただし，その分データ量が多くなるため，基本的にはサンプリング周波数はアナログ信号の最高周波数の2倍（サンプリング周期ならば最低周期の0.5倍）を目安に標本化します。

サンプリング周波数は2倍より高くても問題無いですが，逆に2倍未満だと元データと変換データの差異が大きくなってしまうので，必ず2倍以上で標本化します。

国家試験ではこれさえ覚えておけばAD変換の問題は正解できるから，必ず最高周波数の2倍でサンプリングすることを覚えておいてね。

おるてぃ

量子化（quantization）　

ここからは難しいから参考程度でOK！

おるてぃ

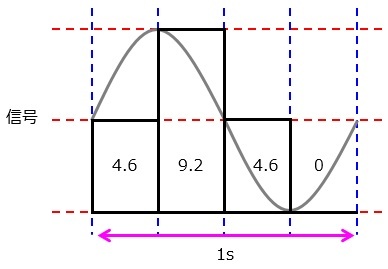
標本化によって得られた値を近似する段階です。
量子化の値を表すのに必要な情報量を量子化bit数といい，量子化bit数が大きいほど，より標本化で得られた値に近い値に量子化することができます。

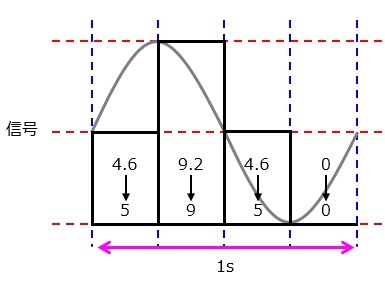
実際に標本化されたデータを見てみましょう。

これを量子化bit数＝4bitで量子化するとなると，16種類の情報を扱えるので，標本化されたそれぞれの値は，
0→0
4.6→5
9.2→10
と量子化できます。

もちろん，量子化bit数を増やせば小数まで扱えるようになるので，4.6は4.6に，9.2は9.2に量子化できるようになります。
（今回は4bitで量子化したことにします。）

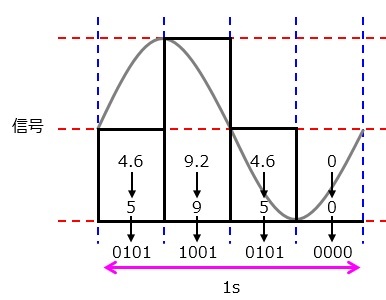
符号化（encode）　

量子化された値を2進数に変換する段階です。
こちらも量子化同様，符号化に用いるbit数が多いほど量子化に近い値を得ることができます。

今回は4bitで符号化してみましょう。

4bitであれば，0～15までは全て符号化できるので，上のデータでは問題なく符号化できることになります。

以上がAD変換の流れとなります。

練習問題

このページの復習だよ。解けるかな？

おるてぃ

問1　A＋B＝Xのとき必ず成立するのはどれか。ただし，＋は論理和を表し，A，B，Xは真理値を示すものとする。（第53回臨床検査技師国家試験am83）

1．A＝0ならばX＝0
2．A＝1ならばX＝0
3．B＝1ならばX＝1
4．X＝1ならばA＝1
5．X＝1ならばB＝1

解答を見る

解答：3
論理和とは言い換えると「OR」ということです。
これさえわかれば，後はOR回路の入出力関係を書き出せば答えは出せます。

入力A	入力B	出力X
0	0	0
0	1	1
1	0	1
1	1	1

1．誤り。Aが0であっても，Bが1であれば，出力Xは1となるので，この命題は偽といえます。（反例：A＝0・B＝1）
2．誤り。Aが1であれば，Bがどのような値を取ろうと出力Xは1となります。
3．正しい。Bが1であれば，Aがどのような値を取ろうと出力Xは1となります。
4．誤り。Xが1であっても，Bが1であればAは0でも1でもよいため，この命題は偽といえます。（反例：A＝0・B＝1）
5．誤り。Xが1であっても，Aが1であればBは0でも1でもよいため，この命題は偽といえます。（反例：A＝1・B＝0）

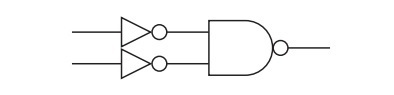
問2　図の回路に相当するゲートはどれか。（第56回臨床検査技師国家試験pm96）

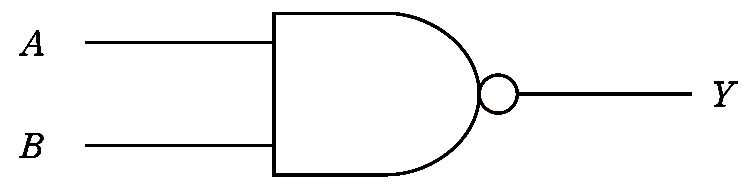
出典：厚生労働省ホームページ　第56回臨床検査技師国家試験の問題及び正答について　午後問題（https://www.mhlw.go.jp/topics/2010/04/dl/tp_siken_56_rinken_03.pdf）

1．AND
2．NAND
3．NOR
4．NOT
5．OR

解答を見る

解答：2
これは簡単ですね。Dの形（AND）＋○（NOT）なので，NANDが正解です。

問3　NOR回路はどれか。（第59回臨床検査技師国家試験pm96）

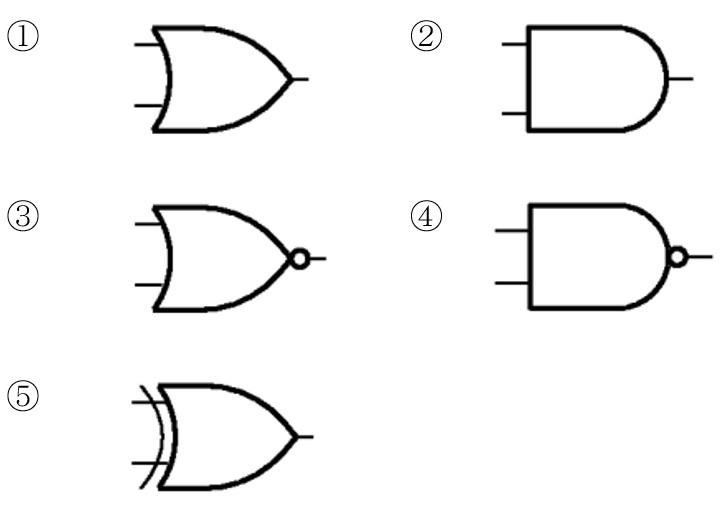
出典：厚生労働省ホームページ　第59回臨床検査技師国家試験の問題及び正答について　午後問題（https://www.mhlw.go.jp/seisakunitsuite/bunya/kenkou_iryou/iryou/topics/dl/tp130422-05c.pdf）

解答を見る

解答：3
各論理回路図を覚えておけば楽々得点できるサービス問題ですね。
1．誤り。OR回路です。
2．誤り。AND回路です（Dの形が特徴）。
3．正しい。OR回路＋○（NOT）なので，NOR回路です。
4．誤り。AND回路＋○（NOT）なので，NAND回路です。
5．誤り。OR回路の入力に線が描かれているものはXOR回路です。

問4　図の回路の入力（A，B）と出力Yの組み合わせで正しいのはどれか。2つ選べ。（第63回臨床検査技師国家試験pm96）

出典：厚生労働省ホームページ　第63回臨床検査技師国家試験の問題及び正答について　午後問題（https://www.mhlw.go.jp/seisakunitsuite/bunya/kenkou_iryou/iryou/topics/dl/tp170425-07b_01.pdf）

1．A＝0，B＝0　→　Y＝0
2．A＝1，B＝0　→　Y＝0
3．A＝0，B＝1　→　Y＝1
4．A＝1，B＝1　→　Y＝0
5．A＝1，B＝1　→　Y＝1

解答を見る

解答：3・4
Dの形（AND）＋○（NOT）なので，問題の回路はNAND回路です。後は，NAND回路の入出力関係さえわかればこの問題はもらったも同然ですね。（NAND自体をすぐに書けなくとも，ANDを書き出せればその出力の0と1を変えるだけなので簡単）

入力A	入力B	出力Y
0	0	1
0	1	1
1	0	1
1	1	0

1．誤り。0，0は1です。
2．誤り。1，0は1です。
3．正しい。0，1は1です。
4．正しい。1，1は0です。
5．誤り。1，1は0です。

問5　真理値表を満たす論理演算回路はどれか。（第28回臨床工学技士国家試験pm59）

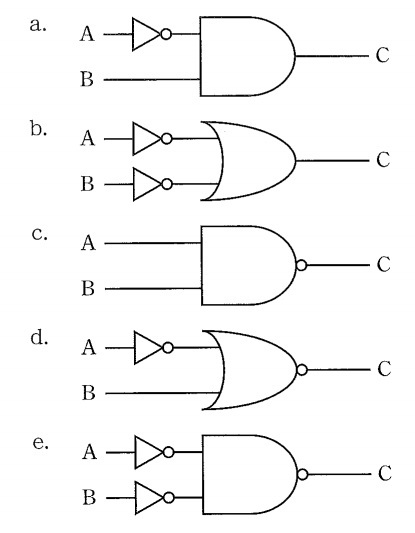
出典：厚生労働省ホームページ　臨床工学技士国家試験問題及び正答肢　第28回午前問題（https://www.jaame.or.jp/rinsyo/siken17/28pm.pdf）

1．a，b
2．a，e
3．b，c
4．c，d
5．d，e

解答を見る

解答：3
真理値表からNAND回路（c）はすぐに選べますが，あと1つはそれぞれ検討していく必要があります。
ただ，cを含む選択肢は3と4の2つしかないので，bの入出力関係を検討して，真理値表の通りになればb，そうでなければdが正しいということになります。
＜bの場合＞
A＝0，B＝0のとき，それぞれNOT回路で1・1となり，これをOR回路に通すので1となります。
A＝1，B＝0（A＝0・B＝1）のとき，それぞれNOT回路で0・1となり，これをOR回路に通すので1となります。
A＝1，B＝1のとき，それぞれNOT回路で0・0となり，これをOR回路に通すので0となります。
よって，真理値表に等しいので，bは正しいということになります。
＜dの場合＞
A＝0，B＝0のとき，AはNOT回路で1となり，これをNOR回路に通すので0となります。
A＝1，B＝0のとき，AはNOT回路で0となり，これをNOR回路に通すので1となります。
A＝0，B＝1のとき，AはNOT回路で1となり，これをNOR回路に通すので0となります。
A＝1，B＝1のとき，AはNOT回路で0となり，これをNOR回路に通すので0となります。
よって，真理値表と異なるので，dは誤りということになります。

したがって，答えは3（b，c）となります。
【参考】
aの回路…A＝0，B＝1のときのみ1，それ以外は0。
eの回路…A＝0，B＝0のときのみ0，それ以外は1。

問6　真理値表に対応する論理演算はどれか。（第29回臨床工学技士国家試験am61）

1．AND演算
2．NAND演算
3．OR演算
4．NOR演算
5．EXOR（exclusive OR）演算

解答を見る

解答：5
2つの入力が等しい時に0，異なるときに1となっているので，EXORが正解となります。

問7　図の回路に等価なのはどれか。（第32回臨床工学技士国家試験pm59）

出典：厚生労働省ホームページ　臨床工学技士国家試験問題及び正答肢　第32回午後問題（https://www.jaame.or.jp/rinsyo/siken17/32pm.pdf）

1．OR
2．AND
3．NOR
4．NOT
5．NAND

解答を見る

解答：1
実際に真理値表を書いてみましょう。

入力A	入力B	出力Y
0	0	0
0	1	1
1	0	1
1	1	1

これより，OR回路と等価とわかるので，1が正解となります。

問8　信号波を示す。パルス振幅変調（PAM）はどれか。（第58回臨床検査技師国家試験am96）

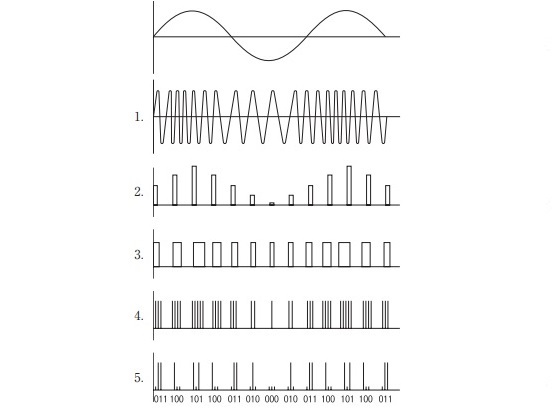
出典：厚生労働省ホームページ　第58回臨床検査技師国家試験の問題及び正答について　午前問題（https://www.mhlw.go.jp/topics/2012/04/dl/tp_siken_58_rinken_am1.pdf）

解答を見る

解答：2
1．誤り。信号がアナログ波で，搬送波の周波数の変化で変調させているので，周波数変調（FM）です。
2．正しい。パルス波の振幅変化で変調しているのでパルス振幅変調（PAM）です。
3．誤り。パルス波の幅（デューティ比）変化で変調しているのでパルス幅変調（PWM）です。
4．誤り。パルス波の数変化で変調しているのでパルス数変調（PNM）です。
5．誤り。パルス波を2進数に変換してから2進数変化で変調しているのでパルス符号変調（PCM）です。

問9　変調後の信号の振幅が変化する変調方式はどれか。（第28回臨床工学技士国家試験pm55）
1．PWM
2．FM
3．PM
4．PAM
5．PCM

解答を見る

解答：4
1．誤り。パルス幅変調（PWM）は幅が変化する変調方式です。
2．誤り。周波数変調（FM）は周波数が変化する変調方式です。
3．誤り。位相変調（PM）は位相が変化する変調方式です。
4．正しい。パルス振幅変調（PAM）は振幅が変化する変調方式です。
5．誤り。パルス符号変調（PCM）は2進数コードが変化する変調方式です。

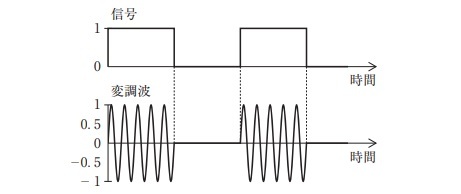
問10　図の変調方式はどれか。（第30回臨床工学技士国家試験am56）

出典：厚生労働省ホームページ　臨床工学技士国家試験問題及び正答肢　第30回午前問題（https://www.jaame.or.jp/rinsyo/siken17/30am.pdf）

1．ASK
2．FSK
3．PSK
4．PWM
5．PPM

解答を見る

解答：1
変調対象がデジタル信号で，変調波の振幅が変化していることから，振幅偏移変調（ASK）が正解となります。

問11　図の変調方式はどれか。（第31回臨床工学技士国家試験pm56）

出典：厚生労働省ホームページ　臨床工学技士国家試験問題及び正答肢　第31回午後問題（https://www.jaame.or.jp/rinsyo/siken17/31pm.pdf）

1．ASK
2．FSK
3．PSK
4．PPM
5．PWM

解答を見る

解答：2
変調対象がデジタル信号で，変調波の周波数が変化していることから，周波数偏移変調（FSK）が正解となります。

問12　正しい組み合わせはどれか。（第32回臨床工学技士国家試験am56）
a．PSK＝位相偏移変調
b．FSK＝周波数分割多重
c．PWM＝パルス振幅変調
d．PPM＝パルス幅変調
e．PCM＝パルス符号変調
1．a，b
2．a，e
3．b，c
4．c，d
5．d，e

解答を見る

解答：2
a．正しい。
b．誤り。FSKは周波数偏移変調です。
c．誤り。PWMはパルス幅変調です。
d．誤り。PPMはパルス位置変調です。
e．正しい。
よって，2．a，eが正解となります。

問13　最高周波数が100Hzである生体信号をAD変換するのに理論上必要となる最長サンプリング周期［s］はどれか。（第55回臨床検査技師国家試験am97）
1．0.005
2．0.01
3．0.1
4．50
5．200

解答を見る

解答：1
AD変換における標本化の際は，サンプリング周波数をアナログ信号の最大周波数の2倍（サンプリング周期はアナログ信号の最低周期の0.5倍）とします。
本問では，最高周波数が100Hzであるため，最低周期は$\frac{1}{100}=0.01$sとなります。よって，必要最長サンプリング周期はこの0.5倍の0.005sとなります。
＜別解　サンプリング周波数から周期を求める＞
本問では，最高周波数が100Hzであるため，必要サンプリング周波数はこの2倍である200Hz。
周期は，周波数の逆数で表すため，あとは必要サンプリング周波数200Hzの逆数を取ればOKです。
よって，$\frac{1}{200}=0.005$sとなります。

問14　最高周波数が100Hzである生体信号をAD変換するのに，理論上使うことができるサンプリング周波数［Hz］の下限はどれか。（第58回臨床検査技師国家試験pm97）
1．10
2．50
3．100
4．200
5．500

解答を見る

解答：4
AD変換における標本化の際は，サンプリング周波数をアナログ信号の最大周波数の2倍とします。
本問では，最高周波数が100Hzであるため，必要サンプリング周波数はこの2倍である200Hzとなります。

問15　0～1kHzの帯域を持つアナログ信号をAD変換するとき，サンプリング定理によって決まるサンプリング間隔［ms］の上限はどれか。（第28回臨床工学技士国家試験pm60）
1．0.2
2．0.5
3．1.0
4．1.5
5．2.0

解答を見る

解答：2
AD変換における標本化の際は，サンプリング周波数をアナログ信号の最大周波数の2倍（サンプリング周期はアナログ信号の最低周期の0.5倍）とします。
本問では，最高周波数が1kHzであるため，最低周期は$\frac{1}{1\,\mathrm{k}}=1$msとなります。よって，必要最長サンプリング周期はこの0.5倍の0.5msとなります。
＜別解　サンプリング周波数から周期を求める＞
本問では，最高周波数が1kHzであるため，必要サンプリング周波数はこの2倍である2kHz。
周期は，周波数の逆数で表すため，あとは必要サンプリング周波数2kHzの逆数を取ればOKです。
よって，$\frac{1}{2\,\mathrm{k}}=0.5$msとなります。

問16　10～70Hzの周波数成分から構成されるアナログ信号をAD変換する。サンプリング周波数［Hz］の下限はどれか。（第30回臨床工学技士国家試験pm61）
1．10
2．20
3．40
4．70
5．140

解答を見る

解答：5
AD変換における標本化の際は，サンプリング周波数をアナログ信号の最大周波数の2倍とします。
本問では，最高周波数が70Hzであるため，必要サンプリング周波数はこの2倍である140Hzとなります。

問17　帯域が1～200Hzのアナログ信号をサンプリングするとき，エイリアシングを起こさないサンプリング間隔の最大値［ms］はどれか。（第32回臨床工学技士国家試験pm60）
1．1
2．1.25
3．2.5
4．5
5．10

解答を見る

解答：3
AD変換における標本化の際は，サンプリング周波数をアナログ信号の最大周波数の2倍（サンプリング周期はアナログ信号の最低周期の0.5倍）とします。
本問では，最高周波数が200Hz（0.2kHz）であるため，最低周期は$\frac{1}{0.2\,\mathrm{k}}=5$msとなります。よって，必要最長サンプリング周期はこの0.5倍の2.5msとなります。
＜別解　サンプリング周波数から周期を求める＞
本問では，最高周波数が200Hzであるため，必要サンプリング周波数はこの2倍である400Hz。
周期は，周波数の逆数で表すため，あとは必要サンプリング周波数400Hzの逆数を取ればOKです。
よって，$\frac{1}{400}=2.5$msとなります。