医療工学解説－交流回路

国家試験で出題される交流回路について解説します！交流回路は難しいので，できるだけ簡単に説明します。

※スマホから閲覧している場合，数式をスクロールできます。

各見出しの重要度は，過去の臨床検査技師国家試験（第52回～最新回まで）の出題率や覚えやすさなどを考慮して主観で表記しています。国家試験を受ける学生以外の方は無視してかまいません。

交流回路の基本（重要度：★★★★☆）
1. 交流回路とは？　
2. 電圧・電流・電力　
リアクタンスとインピーダンス（重要度：★☆☆☆☆）
1. リアクタンス　
2. インピーダンス　
静電容量の合成（重要度：★☆☆☆☆）
1. コンデンサの直列接続　
2. コンデンサの並列接続　
練習問題

交流回路の基本（重要度：★★★★☆）

交流回路とは？　

ペンギンくん

そもそも交流回路って何なの？

「医療工学解説－電気回路」や「医療工学解説－ホイートストンブリッジ・電力」で出てきた回路は全て直流回路と言って，これは電圧が一定の回路だったんだ。今回勉強する交流回路は，電圧が時間によって変化するという，ちょっと変わった回路なんだよ。

おるてぃ

「医療工学解説－電気回路」および「医療工学解説－ホイートストンブリッジ・電力」で出てきた回路は，全ての電源の記号にが使われていました。これは，「直流」を意味していて，電圧が時間経過によって変化しないものです。対して，今回対象とする「交流」は，電圧が時間経過によって変化する回路です。

図1　交流回路の電圧変化（縦軸が電圧・横軸が時間を表す）

ペンギンくん

へぇ～，きれいな曲線だね。

この曲線のことをサインカーブと呼ぶんだよ。
あっ，そうそう，まだ「医療工学解説－電気回路」・「医療工学解説－ホイートストンブリッジ・電力」の記事を見ていない人はこちらも参照してみてね！

おるてぃ

医療工学解説－電気回路

国家試験で出題される電気回路について解説します！電気回路の計算が苦手な方必見！

医療工学解説－ホイートストンブリッジ・電力

国家試験で出題されるホイートストンブリッジと電力計算について解説します！これらの計算が苦手な方は見る価値ある……かも？

電圧・電流・電力　

ペンギンくん

交流回路ではどう電圧を求めればいいの？

交流回路では，最大値と実効値という電圧の値が出てくるから，まずこれを覚えておこう！

おるてぃ

直流なら電圧は定義されているものそのものですが，電圧の変化する交流はどう考えればいいのでしょうか？

交流では，電圧の最大値と実効値というものだけを覚えておけばOKです。なお，交流回路の問題が出題されることはまずないので，最大値と実効値だけを全力で覚えましょう。

電圧の最大値

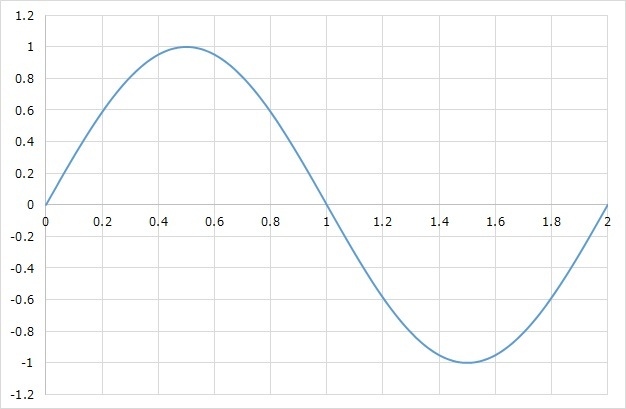
最大値は単純に，グラフのうち最も電圧の大きな値を取る点です。

図2　交流回路の電圧の最大値

このグラフ（$y=\,\mathrm{sin}\pi x$）なら，時間が0.5s経過時に最大の1.0を取ります。

電圧の実効値

実効値は以下のように定義されています。

ある電気抵抗に交流電圧を加えた場合の1周期における平均電力と、同じ抵抗に直流電圧を加えた場合の電力が, 互いに等しくなるときに、この交流電圧と交流電流の実効値はそれぞれ, その直流電圧と直流電流と同じ値であると定義される。
引用：フリー百科事典『ウィキペディア（Wikipedia）』
（https://ja.wikipedia.org/wiki/%E5%AE%9F%E5%8A%B9%E5%80%A4）

上の説明だと難しいのですが，簡単に言えば，直流と同じ電力を発生させる交流電圧の値ということになります。

実際には，実効値の意味はそこまで知っておく必要はなく，むしろ以下の式を覚えておきましょう。

電圧実効値＝電圧最大値$\times \frac{1}{\sqrt{2}}$
（電圧最大値＝電圧実効値$\times \sqrt{2}$）

なお，家庭用の商用交流で書かれている「100V」などは，実効値を表しています。なので，家庭用商用交流の電圧最大値は$100\times \sqrt{2}\approx 141\,\mathrm{V}$となります。

電流の最大値と実効値

電流の最大値は，電圧が最大値を取るときに流れる電流の値となります。
同様に，電流の実効値は，電圧が実効値を取るときに流れる電流の値となります。

電流においても，以下の式が成り立ちます。

電流実効値＝電流最大値$\times \frac{1}{\sqrt{2}}$
（電流最大値＝電流実効値$\times \sqrt{2}$）

平均電力

平均電力は，電圧が実効値を取るときに消費される電力のことです。
実際に問題を解いてみましょう。

例題1：交流回路において，電圧の最大値がV，電流の最大値がIのとき，平均電力P［W］はいくらか。

電圧と電流のそれぞれの実効値V_e，I_eは

$$V_e=V\times \frac{1}{\sqrt{2}}$$

$$I_e=I\times \frac{1}{\sqrt{2}}$$

平均電力は電圧が実効値を取るときに消費される電力のことであるため，

$$\bar{P}=V_e\times I_e=\frac{V}{\sqrt{2}}\times \frac{I}{\sqrt{2}}=\frac{1}{2}IV$$

となります。

リアクタンスとインピーダンス（重要度：★☆☆☆☆）

ペンギンくん

リアクタンス？インピーダンス？？もう意味不明すぎてヤバイ。

まあまあ，落ち着いて。できる限りわかりやすく説明してあげるから。

おるてぃ

「リアクタンス」と「インピーダンス」。あまり耳にしないワードが出てきました。
最初は意味不明に聞こえるかもしれませんが，意外と簡単です。では，順に説明していきます。

リアクタンス　

リアクタンスとは，簡単に言えば，交流回路でのコンデンサやコイルの電流の通しにくさのことを指します。つまり，コンデンサやコイルを抵抗とみなした時の抵抗値のことです。単位はΩ。

単位を忘れていたという人は「医療工学解説－単位」で復習しておいてね！

おるてぃ

※コンデンサ：電気をためたり放電したりする電子部品。キャパシタとも呼ばれる。
　コイル：電流を安定化させたり，電圧を変化させる電子部品（他にも様々な役割があるが割愛）。インダクタとも呼ばれる。

医療工学解説−単位

医療工学の分野でよく出題されるSI単位・SI接頭辞・SI組立単位について説明します！単位があいまいな方必見！

コイルのリアクタンスのことを誘導性リアクタンス，コンデンサのリアクタンスのことを容量性リアクタンスといいます。

ここまではわかりやすいですが，問題はこの求め方が結構厄介ということです。

【誘導性リアクタンス】

$$X_L=2\pi fL$$

X_L：コイルのリアクタンス［Ω］
f：電源の周波数［Hz］
L：インダクタンス［H（ヘンリー）］

【容量性リアクタンス】

$$X_C=\frac{1}{2\pi fC}$$

X_C：コンデンサのリアクタンス［Ω］
f：電源の周波数［Hz］
C：静電容量［F（ファラド）］

ペンギンくん

これ…覚えないとダメ？

余裕があれば覚えておきたいけど，国家試験にはまだ出題されてないから優先度は低めかな。

おるてぃ

ペンギンくん

（よかった～，覚えないでおこっと。）

インピーダンス　

インピーダンスとは，抵抗とリアクタンスをひっくるめた総称のことです。単位はΩ。

抵抗のみの場合はインピーダンス＝抵抗値。
コイルのみの場合はインピーダンス＝誘導性リアクタンス。
コンデンサのみの場合はインピーダンス＝容量性リアクタンス

となります。
2つ以上ある場合のインピーダンスは計算が必要ですが，これは単純な足し算では求まりません。以下の公式に当てはめる必要があります。
※国試では直列回路しか出題されないので，直列回路の公式のみを示します。

【RL（抵抗－コイル）直列回路】

$$Z_{RL}=\sqrt{R^2+X_L^2}$$

Z_RL：RL直列回路のインピーダンス［Ω］
R：抵抗値［Ω］
X_L：コイルのリアクタンス［Ω］

【RC（抵抗－コンデンサ）直列回路】

$$Z_{RC}=\sqrt{R^2+X_C^2}$$

Z_RC：RC直列回路のインピーダンス［Ω］
R：抵抗値［Ω］
X_C：コンデンサのリアクタンス［Ω］

【LC（コイル－コンデンサ）直列回路】

$$Z_{LC}=X_L-X_C$$

Z_LC：LC直列回路のインピーダンス［Ω］
L：コイルのリアクタンス［Ω］
X_C：コンデンサのリアクタンス［Ω］

【RLC（抵抗－コイル－コンデンサ）直列回路】

$$Z_{RLC}=\sqrt{R^2+(X_L-X_C)^2}$$

Z_RL_C：RC直列回路のインピーダンス［Ω］
R：抵抗値［Ω］
X_L：コイルのリアクタンス［Ω］
X_C：コンデンサのリアクタンス［Ω］

なお，ここではインピーダンスの話をしましたが，電圧に置き換えても上の式は成り立ちます。

例えば，RL直列回路で，抵抗値にかかる電圧がV_R，コイルにかかる電圧がV_Lとすると，全体の回路の電圧E［V］は

$$E=\sqrt{V_R^2+V_L^2}$$

となります。

【RLC直列共振回路】
RLC直列回路では，共振と呼ばれる状態になることがあります。共振回路では，コイルのリアクタンスX_LとコンデンサのリアクタンスX_Cが等しくなる（X_L＝X_C）ため，回路のインピーダンスは抵抗値に等しくなります。

$$Z_{RLC}=R$$

簡単に言うと，コイルとコンデンサの存在を無視することができるということなんだよ。

おるてぃ

例題2：回路図を図3に示す。この回路のインピーダンス［Ω］はいくらか。

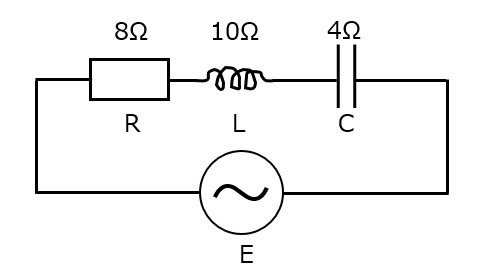
図3

初めて出てくる記号があると思いますが，記号自体は簡単です。
：交流電源
：コイル
：コンデンサ

これさえわかれば，後はインピーダンスの式にそれぞれの抵抗値（リアクタンス）を代入すればOKです。よって，回路全体のインピーダンスZは

$$Z=\sqrt{R^2+(X_L-X_C)^2}=\sqrt{8^2+(10-4)^2}=\sqrt{100}=10\,\mathrm{Ω}$$

となります。

ペンギンくん

計算自体は簡単だね！

問題は，この公式を覚えることが面倒…ってことかな。

おるてぃ

静電容量の合成（重要度：★☆☆☆☆）

ペンギンくん

静電容量って何？

静電容量はどのくらい電気を貯められるかを表す言葉だよ。主にコンデンサで使われるよ。

おるてぃ

静電容量とは，コンデンサなどにおいて，どれだけ電荷を蓄えられるか，つまりどれだけ電気を貯められるかを表す言葉です。単位はF（ファラド）。

コンデンサは，1個単独ではそのコンデンサの静電容量がそのまま適応されますが，コンデンサを2個以上つなぐと全体の静電容量が変わります。この場合は，コンデンサを1個とみなすことで，静電容量を求めることができます。

このときの静電容量を合成静電容量と呼びます。

ペンギンくん

抵抗と同じ感じだね。

そう！合成抵抗の求め方が頭にあれば簡単に求められるよ。合成抵抗の計算については「医療工学解説－電気回路」を参照してね！

おるてぃ

医療工学解説－電気回路

国家試験で出題される電気回路について解説します！電気回路の計算が苦手な方必見！

コンデンサの直列接続　

実際に回路を見ながら考えていきましょう。

例題3：回路図を図4に示す。コンデンサの合成静電容量［F］はいくらか。

図4

直列に接続されたコンデンサの場合は，以下の公式で合成静電容量を求めることができます。並列接続の合成抵抗を求めるときと同じ計算です。

【直列での合成静電容量】

$$C_s=\frac{1}{\frac{1}{C_1}+\frac{1}{C_2}+\frac{1}{C_3}+\cdots+\frac{1}{C_n}}$$

C_s：直列の合成静電容量［F］
C₁～C_n：各コンデンサの静電容量（n個）［F］

もちろん，コンデンサ2つの場合は和分の積が利用できます。

$$C_s=\frac{C_1\times C_2}{C_1+C_2}$$

ペンギンくん

なるほど！コンデンサの場合は直列がこの式になるんだね。

合成抵抗の求め方が頭に入っていれば覚えやすいはず。

おるてぃ

図4の場合は静電容量がそれぞれ20μF・5μFであるため，合成静電容量C_sは

$$C_s=\frac{20\mu\times 5\mu}{20\mu+5\mu}=4\mu\,\mathrm{F}$$

となります。

コンデンサの並列接続　

こちらは単純に各コンデンサの静電容量を足すだけでOKです。

【並列での合成静電容量】

$$C_p=C_1+C_2+C_3+\cdots+C_n$$

C_p：並列の合成静電容量［F］
C₁～C_n：各コンデンサの静電容量（n個）［F］

練習問題

このページの復習だよ。解けるかな？

おるてぃ

問1　交流回路における，電圧および電流の最大振幅値の積に対する平均電力の割合として正しいのはどれか。（第58回臨床検査技師国家試験pm95）

1．$\frac{1}{2}$
2．$\frac{1}{\sqrt{2}}$
3．1
4．$\sqrt{2}$
5．2

解答を見る

解答：1
平均電力とは，電圧・電流が実効値のときの電力のことをいいます。今回の問題では，電圧と電流の最大値の積と平均電力の比率を問うているため，それぞれを求めて比を取ればOKです。
電圧最大値をV，電流最大値をI，電圧実効値をV_e，電流実効値をI_eとすると，電圧と電流の最大値の積P_maxは$P_{max}=IV$，平均電力Pは$P=I_eV_e$と表せます。
これより，それぞれの比$\frac{P}{P_{max}}$は

$$\frac{P}{P_{max}}=\frac{I_eV_e}{IV}　(1)$$

となります。
次に，最大値＝実効値$\times \sqrt{2}$を使いましょう。

$$I=\sqrt{2} I_e　(2)$$

$$V=\sqrt{2} V_e　(3)$$

最後に，（2）・（3）を（1）に代入すればいいので，答えは

$$\frac{P}{P_{max}}=\frac{I_eV_e}{\sqrt{2} I_e\times \sqrt{2} V_e}=\frac{1}{2}$$

となります。

問2　商用交流100Vが表しているのはどれか。（第60回臨床検査技師国家試験pm95）

1．最大値
2．実効値
3．瞬時値
4．測定値
5．平均値

解答を見る: 解答：2
交流回路の電圧は，基本的には実効値で表示するので，商用交流100Vは実効値ということになります。
なお，最大値は実効値$\times \sqrt{2}$，平均値は最大値$\times \frac{2}{\pi}$となります。

問3　RLC直列回路において共振時の電気インピーダンスの大きさはどれか。ただし，$\omega$は共振角周波数とする。（第32回臨床工学技士国家試験pm49）

1．R
2．$\frac{1}{\omega C}$
3．$\omega L$
4．$\omega L+\frac{1}{\omega C}$
5．$\frac{1}{\sqrt{LC}}$

解答を見る: 解答：1
RLC直列共振回路では，インピーダンスは抵抗値に等しくなるため，Z＝Rとなります。

問4　RLC直列回路のインピーダンス［Ω］はどれか。ただし，抵抗器の抵抗値は4Ω，誘導性リアクタンスは7Ω，容量性リアクタンスは4Ωとする。（第61回臨床検査技師国家試験am96）

1．2
2．5
3．7
4．11
5．15

解答を見る

解答：2
RLC直列回路のインピーダンスは以下の計算式で求まります。

$$Z_{RLC}=\sqrt{R^2+(X_L-X_C)^2}$$

※X_Lはコイルのリアクタンス＝誘導性リアクタンス
X_Cはコンデンサのリアクタンス＝容量性リアクタンス
よって，

$$Z_{RLC}=\sqrt{4^2+(7-4)^2}=5Ω$$

となります。

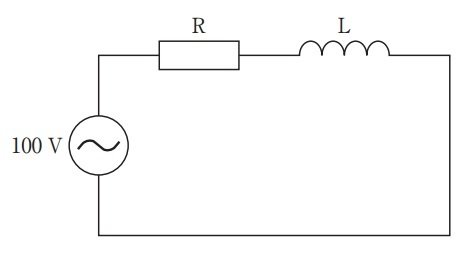
問5　図の正弦波交流回路で抵抗Rの両端の電圧が60Vのとき，コイルLの両端の電圧［V］はどれか。（第30回臨床工学技士国家試験pm50）

出典：厚生労働省ホームページ　臨床工学技士国家試験問題及び正答肢　第30回午後問題（https://www.jaame.or.jp/rinsyo/siken17/30pm.pdf）

1．0
2．20
3．40
4．60
5．80

解答を見る

解答：5
RL回路のインピーダンスは以下の式で求めます。

$$Z_{RL}=\sqrt{R^2+X_L^2}$$

インピーダンスと同様，電圧も同じ式を使えます。
回路全体の電圧が100V，Rの電圧が60Vであるため，

$$100=\sqrt{60^2+V_L^2}$$

$$V_L^2=10000-3600=6400$$

$$V_L=80\,\mathrm{V}$$

となります。