医療工学解説－ホイートストンブリッジ・電力

国家試験で出題されるホイートストンブリッジと電力計算について解説します！これらの計算が苦手な方は見る価値ある……かも？

※スマホから閲覧している場合，数式をスクロールできます。

各見出しの重要度は，過去の臨床検査技師国家試験（第52回～最新回まで）の出題率や覚えやすさなどを考慮して主観で表記しています。国家試験を受ける学生以外の方は無視してかまいません。

ホイートストンブリッジ（重要度：★★★☆☆）

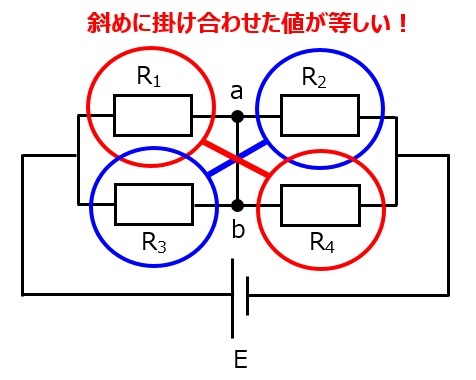
ホイートストンブリッジとは，直列2個の抵抗が並列接続されていて，並列回路の途中で，1つの導線によって再結合している回路のことです。

この回路で，並列抵抗間（a-b間）が等電位，つまり，導線a-b間に流れる電流が0のとき，以下のような式が成り立ちます。
※なお，この条件を平衡条件といい，平衡条件を満たしている状態を平衡状態といいます。

これはつまり，抵抗値を斜めに掛け合わせた値が等しいということです。

なお，a-b間に抵抗があったとしても，平衡状態のときは，その抵抗を無視することができます。

この公式が成り立つ理由についてはここでは言及しません。気になる方は，「ホイートストンブリッジ」で検索してみてください。（いろいろな方が詳しく説明してくださっています）

次は，実際に数値を入れた状態で見てみましょう。

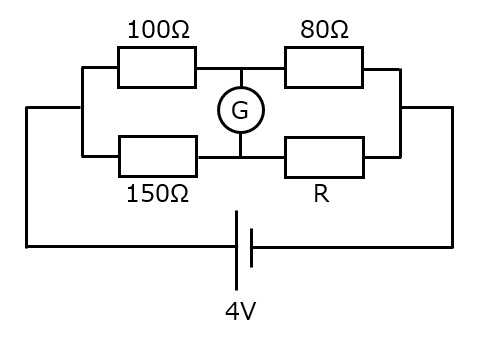
図2

回路中のGは検流計で，微弱な電流を検出するのに使われます。
並列抵抗間に流れる電流が0（＝平衡状態）であるため，上記の式より，$$100\times R=80\times 150$$

となります。

電力計算（重要度：★★★☆☆）

基本的な電力の求め方　

電力とは，単位時間に電流がする仕事量のことです。ただ，この意味を覚えるよりも，実際に電力を求める公式を覚えておきましょう。

公式自体は簡単で，電圧と電流の積から電力を求めることができます。

実際に回路を見てみましょう。

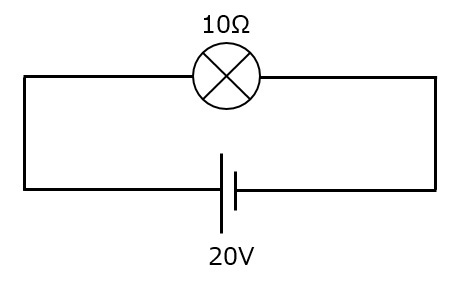
図3

⊗は豆電球を示しています。この豆電球の消費電力を求めてみましょう。
まずは，回路を流れる電流Iをオームの法則で求めます。
（オームの法則については医療工学解説－電気回路を参照）

電流を求められましたので，最後に，電圧と電流を掛け合わせます。よって，

となります。

抵抗値変化による電力の求め方　

電力は，先ほど示したP=EIの式で求められますが，抵抗値が変わると電流Iも変化するため，そこに注意して電力を求める必要があります。実際に例題を見てみましょう。

まず，電気抵抗の求め方について確認しておきましょう。

この式は丸々覚えなくてもいいのですが，電気抵抗はその物質の長さに比例し，断面積に反比例するということは必ず覚えておきましょう！

では，実際に問題を解いていきましょう。

電圧100Vで200Wの電力を消費するので，ここを流れる電流Iは

これより，この電熱器の抵抗値Rは

本問では本数が2倍＝断面積が2倍になっているので，抵抗値は$\frac{1}{2}$となるため，本数が2倍となった時の抵抗値R’は

後は，R’のときの電流I’を求めてから電力Pを求めればOKです。よって，

となります。

電圧変化による電力の求め方

電力は，先ほど示したP=EIの式で求められますが，電圧が変わると電流Iも変化するため，そこに注意して電力を求める必要があります。実際に例題を見てみましょう。

まずはこの電熱器の抵抗値を求めます。

次に，この抵抗に50Vの電圧をかけた時の電流I’を求めます。$$I’=\frac{E’}{R}=\frac{50}{50}=1\,\mathrm{A}$$最後に，電圧（変圧後）と電流（変圧後）を掛け合わせればOKなので，

となります。

注意したいのは，最初で求めた電流（本問では2A）と変圧後の電圧（本問では50V）をそのまま掛け合わせてはいけないということです。必ず抵抗を求めてから変圧後の電流を求める手順が必要です。

練習問題

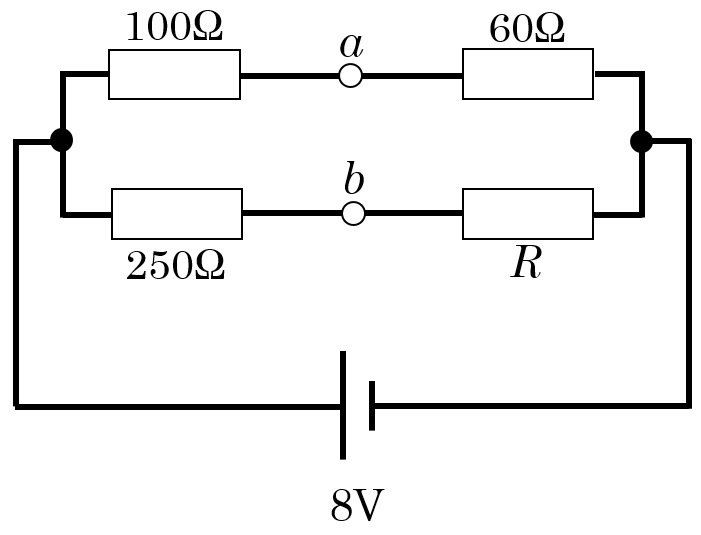
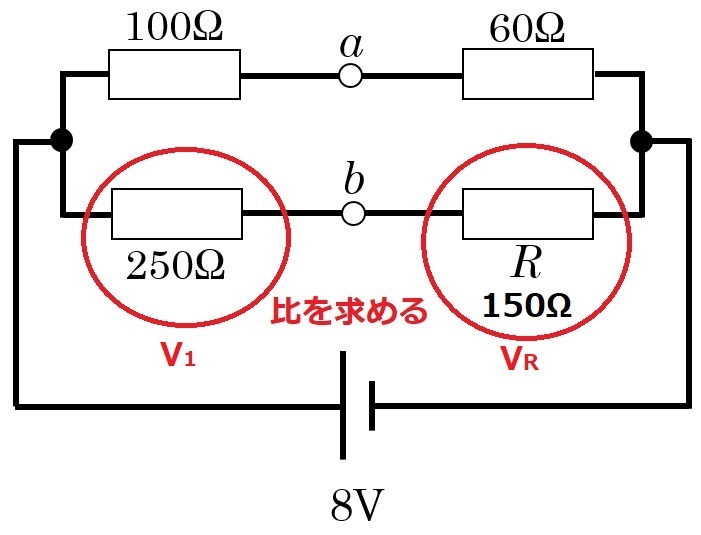
問1　抵抗4個を接続した直流回路を図に示す。回路のa-b間の電位差が0Vであるとき，抵抗Rの両端電圧[V]はどれか。（第60回臨床検査技師国家試験am96）

1．1.0
2．1.5
3．2.0
4．2.5
5．3.0

解答を見る

解答：5
回路を見て，a-b間の電位差が0Vであることから，平衡状態のホイートストンブリッジと気が付ければ解答は容易です。
まず，平衡状態のホイートストンブリッジの公式より，

$$100\times R=60\times 250$$

$$R=150Ω$$

次に，250ΩとR（150Ω）の部分に注目します。

 

この2つの電圧比は抵抗比に等しいことから，

$$V_1:V_R=250:150=5:3$$

並列回路にかかる電圧は等しいので，下の直列部分にかかる電圧は8V。

 

よって，

$$V_R=8\times \frac{3}{5+3}=3\,\mathrm{V}$$

となります。

【別解】オームの法則を用いてRの両端電圧を求める
※R=150Ωを求めるところまでは同じです。
250ΩとRの直列部分の合成抵抗は400Ω。
そこにかかる電圧は8Vであるため，流れる電流は

$$I=\frac{8}{400}=20\,\mathrm{mA}$$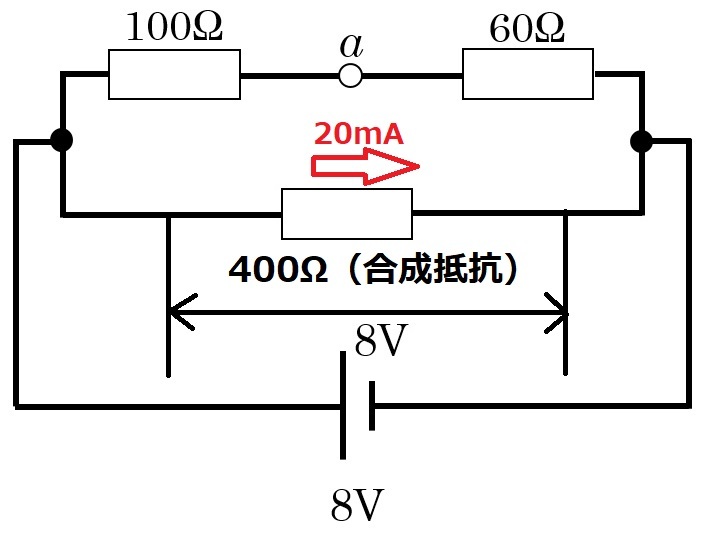

直列部分に流れる電流は一定であることから，Rにかかる電圧V_Rは

$$V_R=20\,\mathrm{m}\times 150=3000\,\mathrm{mV}=3\,\mathrm{V}$$

ホイートストンブリッジの知識だけでなく，医療工学解説－計算1（電気回路）で述べた知識も必要となるので，わからない部分があれば確認しておいてくださいね。

 

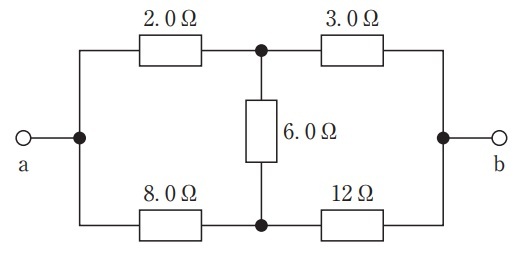
問2　図のab間の合成抵抗［Ω］はどれか。（第32回臨床工学技士国家試験am50）

1．1.0
2．2.0
3．3.0
4．4.0
5．5.0

解答を見る

解答：4
回路を見て，まずはホイートストンブリッジの平衡条件を満たすかどうかを確かめます。
すると，$2\times 12=3\times 8$が成り立つので，平衡状態であることが分かります。この場合，真ん中にある抵抗（6.0Ω）は完全に無視できるので，以下のように回路を変換できます。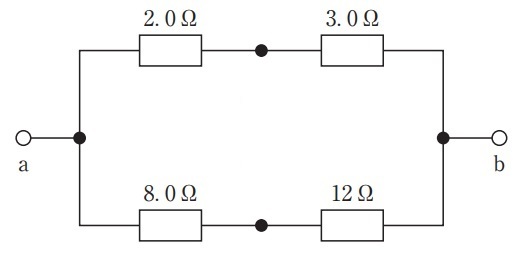

こうなれば，基本的な合成抵抗の求め方の図になるので，後は，直列部分→並列部分と合成抵抗を求めればOKです。
直列部分は，上側が5Ω，下側が20Ω。
よって，回路全体の合成抵抗は

$$R=\frac{5\times 20}{5+20}=\frac{100}{25}=4Ω$$

となります。

 

問3　電圧100Vで500Wの電熱器がある。電圧を変えずに針金の長さを半分にした場合の電力はどれか。（第56回臨床検査技師国家試験pm95）

1．125W
2．250W
3．500W
4．1,000W
5．2,000W

解答を見る

解答：4
まずは電熱器の抵抗値を求めます。

$$I=\frac{P}{E}=\frac{500}{100}=5\,\mathrm{A}$$

$$R=\frac{E}{I}=\frac{100}{5}=20Ω$$

針金の長さと抵抗値は比例するため，針金の長さが0.5倍になれば抵抗値も0.5倍。よって，針金の長さを半分にした時の電熱器の抵抗R’はR’＝10Ω。この時に流れる電流I’は

$$I’=\frac{E}{R’}=\frac{100}{10}=10\,\mathrm{A}$$

ゆえに，電力P’は

$$P’=EI’=100\times 10=1000\,\mathrm{W}$$

となります。

 

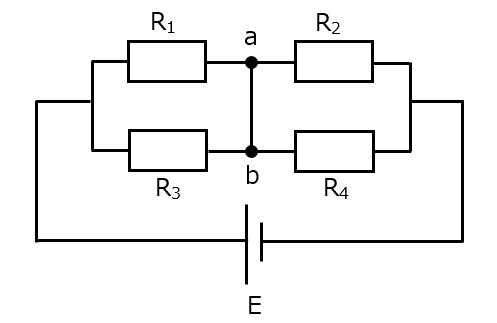
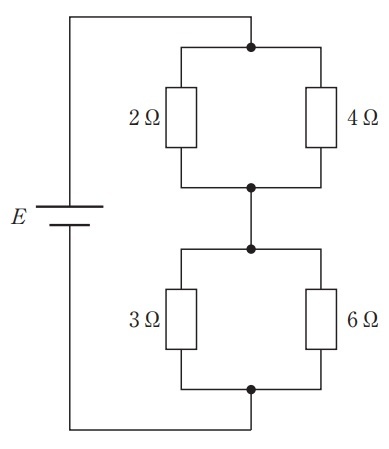
問4　図の回路で2Ωの抵抗の消費電力が2Wである。電源電圧E［V］はどれか。（第29回臨床工学技士国家試験pm46）

1．2
2．3
3．4
4．5
5．6

解答を見る

解答：4
抵抗値のみわかっていて，電圧と電流が分からない状況です。ただ，2Ωの抵抗の消費電力が分かっているので，後はここにかかる電圧がわかれば一気に解けそうですね。
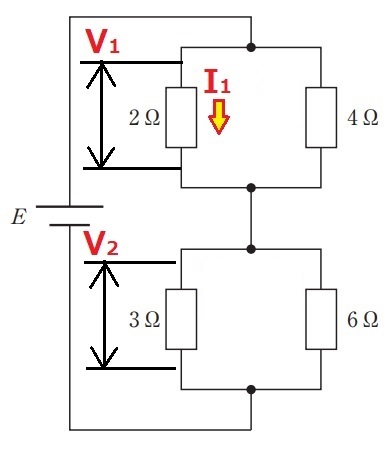
ということで，まずは図のように電圧と電流を定義し，V₁から求めていきます。

オームの法則より，

$$I_1=\frac{V_1}{2}$$

電力を求める式より，

$$P=V_1I_1=\frac{V_1^2}{2}$$

$$2=\frac{V_1^2}{2}$$

$$V_1=2\,\mathrm{V}$$

次に，並列部分のそれぞれの合成抵抗を求めていきます。
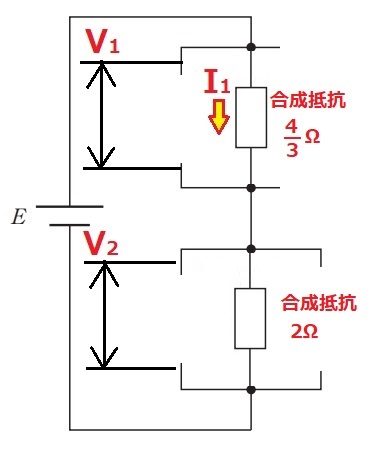
上側の合成抵抗R₁は

$$R_1=\frac{2\times 4}{2+4}=\frac{4}{3}Ω$$

下側の合成抵抗R₂は$$R_2=\frac{3\times 6}{3+6}=2Ω$$

 

直列回路では，抵抗比＝電圧比であるから

$$V_1:V_2=\frac{4}{3}:2=2:3$$

V₁=2Vより，V₂=3V。
よって，電源電圧$E＝V_1+V_2=5\,\mathrm{V}$となります。