国家試験で出題される2進数・16進数の計算について解説します!これらの計算が苦手な方は必見!?(+bitの計算も解説!)
※スマホから閲覧している場合,数式をスクロールできます。
各見出しの重要度は,過去の臨床検査技師国家試験(第52回~最新回まで)の出題率や覚えやすさなどを考慮して主観で表記しています。国家試験を受ける学生以外の方は無視してかまいません。
2進数(重要度:★★★★☆)
2進数とは


2進数という言葉は聞いたことがある人も多いかもしれません。
これは,全ての数値を0と1の組み合わせで表現したものです。
普段私たちが日常で使っているのは10進数と言って,これは数値を0~9の10個の数字を使って表現しています。
(そのため,9の次は10(位が1つ増えて,もとあった位は0になる)となります)
2進数もこれと同じように,1の次は2ではなく,位が1つ増えてもとあった位は0となるため,10となります。
2進数と10進数の対応は以下のようになります。
| 10進数 | 2進数 | 10進数 | 2進数 |
| 0 | 0 | 6 | 110 |
| 1 | 1 | 7 | 111 |
| 2 | 10 | 8 | 1000 |
| 3 | 11 | 9 | 1001 |
| 4 | 100 | 10 | 1010 |
| 5 | 101 | … | … |


2進数の変換


国家試験でこの変換の問題はまだ出題されていないのですが,2進数の計算でこの変換を知っておくと,計算結果が正しいかどうかを確認できるので,変換方法を覚えておきましょう!
2進数→10進数変換
2進数から10進数への変換方法は以下の通りです。
2進数の数値の右からn番目の数値に2n-1をそれぞれ掛け合わせて,それぞれの数値を足し合わせる。
言葉だとわかりづらいので,実際にやってみましょう。
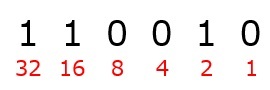
まずは2進数の値である110010を紙に書き出しましょう。
次に,数値の右から1,2,4……と2n-1の値を下に書きましょう。
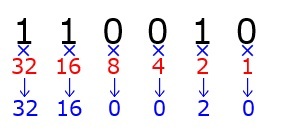
次に,上の数字(黒)と,下の数字(赤)を掛け合わせます。
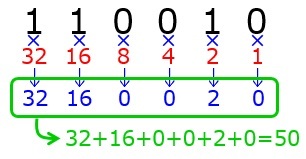
最後に,掛け合わせた数字(青)を足し合わせます。これが,10進数に変換したときの値となります。
よって,2進数で110010は10進数で表すと50となります。


10進数→2進数変換
2進数から10進数への変換では2を掛けていましたが,10進数から2進数への変換は逆に2で割っていきます。
10進数の数値を2で割り,商を右に,余りを商の下に書く。これを,商が0になるまで行い,最後に余りを右から左に読み上げる。
これも言葉だけだとちんぷんかんぷんなので,実際に例題を見ていきましょう。
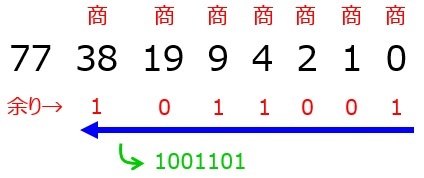
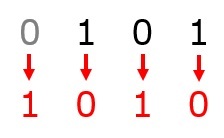
まずは10進数の値である77を紙に書き出しましょう。
次に,77を2で割ります。すると,商が38,余りが1となります。この商を右に,余りを商の下に書きます。
同様にして,どんどん2で割っていきます。
最後に,余りを右から左に向かって読みます。これが2進数に変換したときの値となります。
よって,10進数で77は2進数で表すと1001101となります。


2進数の計算


2進数の計算は国家試験に出題されるので計算方法を覚えましょう。ただ,この方法を知らなくても,2進数を一旦10進数に変換して,これでいつも通りの10進数の計算をして,再度10進数を2進数に変換する方法でも計算できます。新しいことを覚えたくない人は,こちらの方法で。
2進数の足し算
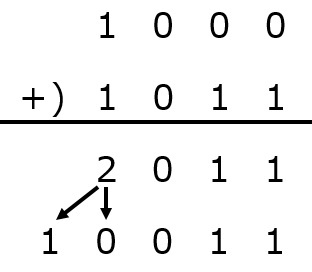
10進数と同じように足し算を行います。その後,2以上は2進数に変換してからまた足し算します。これを,0と1だけになるまで行います。
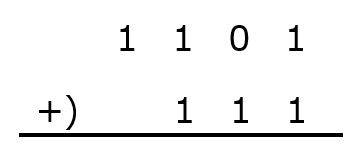
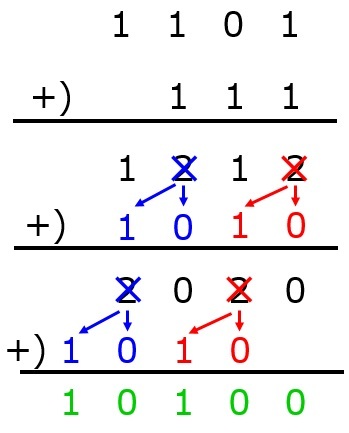
実際に計算してみましょう。
まずは,小学校で習った筆算のように書きます。
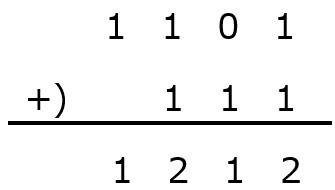
次に,10進数の要領で普通に計算します。
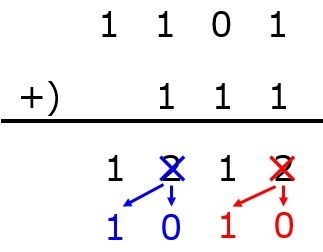
ここで,2進数は0と1の2つの数値しか扱わないので,2以上の数値は2進数で表しましょう。
これでまた足し算します。
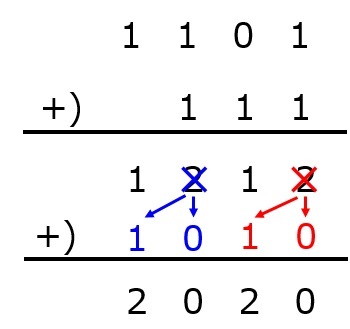
後は,「2以上の値が出た時は2進数の値に変える→計算する」を繰り返して,0と1の値だけになるようにします。
よって,2進数で1101と111を加えた値は10100となります。


上で示した計算方法が面倒な場合は,10進数に変換してから計算するのがおすすめです。
2進数:1101→10進数:8+4+0+1=13
2進数:111→10進数:4+2+1=7
この値を足し合わせます。13+7=20
最後に,20を2進数に変換します。
※( )は余りを表します。
20→10(0)→5(0)→2(1)→1(0)→0(1)
よって,10100となります。

2進数の引き算
2進数の引き算はやや厄介です。ここでは補数を使った方法を紹介します。
言葉だと説明しづらいので,こちらも実際に計算してみましょう。
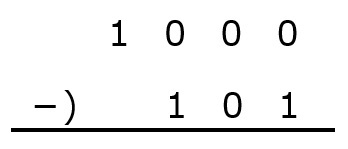
まずは,小学校で習った筆算のように書きます。
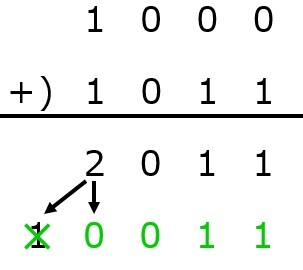
次に,引く数(ここでは101)の補数を求めます。補数は簡単で,もとの数字のそれぞれの位を見て,1なら0,0なら1にすればOKです。
なお,注意点として,補数を求める際は,引かれる側の数(ここでは1000)の桁数と同じになるように,引く数をみなす必要があります。なので,101は,0101として補数を考えます。
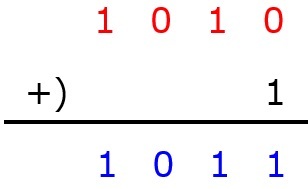
次に,この補数に1を足します。
次に,引かれる側の値(1000)と,先ほど出した補数+1(1011)を足し合わせます。
最後に,一番上の位の1を消すと答えになります。
よって,2進数で1000から101を引いた値は11となります。


上で示した計算方法が面倒な場合は,10進数に変換してから計算するのがおすすめです。
2進数:1000→10進数:8+0+0+0=8
2進数:101→10進数:4+0+1=5
引き算をします。8-5=3
最後に,3を2進数に変換します。
※( )は余りを表します。
3→1(1)→0(1)
よって,11となります。

16進数(重要度:★☆☆☆☆)
16進数とは


16進数は,全ての数値を0~9と,アルファベットA~Fの組み合わせで表現したものです。
16進数の場合,9の次はAとなり,以降,B→C→D→E→F→10(位が1つ増える)となります。
16進数と10進数の対応は以下の通りです。
| 10進数 | 16進数 | 10進数 | 16進数 |
| 0 | 0 | 10 | A |
| 1 | 1 | 11 | B |
| 2 | 2 | 12 | C |
| 3 | 3 | 13 | D |
| 4 | 4 | 14 | E |
| 5 | 5 | 15 | F |
| 6 | 6 | 16 | 10 |
| 7 | 7 | 17 | 11 |
| 8 | 8 | 18 | 12 |
| 9 | 9 | … | … |


16進数の変換
16進数→10進数変換
16進数から10進数への変換方法は以下の通りです。やり方自体は2進数と同じなので,2進数→10進数の変換が理解できていれば簡単です。
16進数の数値の右からn番目の数値に16n-1をそれぞれ掛け合わせて,それぞれの数値を足し合わせる。
せっかくなので,例題を見てみましょうか。
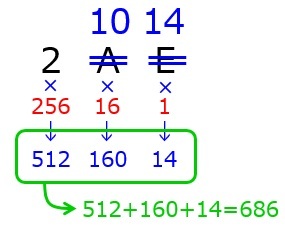
まずは2進数の値である2AEを紙に書き出しましょう。
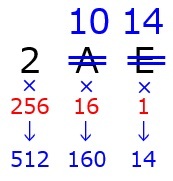
次に,数値の右から1,16,256……と16n-1の値を下に書きましょう。
次に,上の数字(黒)と,下の数字(赤)を掛け合わせます。ここで注意したいのは,A~Fです。これらは,10進数の値に必ず変えておきましょう!
A=10,B=11,C=12,D=13,E=14,F=15(これはどこかしらにメモっておくといいかも)
最後に,掛け合わせた数字(青)を足し合わせます。これが,10進数に変換したときの値となります。
よって,16進数で2AEは10進数で表すと686となります。


10進数→16進数変換
こちらも10進数から2進数への変換方法と同じなので,10進数→2進数の変換が理解できていれば簡単です。
10進数の数値を16で割り,商を右に,余りを商の下に書く。これを,商が0になるまで行う。余りのうち,10~15はそれぞれA~Fに変換し,最後に余りを右から左に読み上げる。
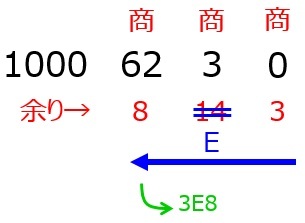
実際に例題を見ていきましょう。
まずは10進数の値である1000を紙に書き出しましょう。
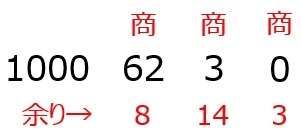
次に,1000を16で割ります。すると,商が62,余りが8となります。この商を右に,余りを商の下に書きます。
同様にして,どんどん16で割っていきます。
次に,余り10~15を16進数に変換します。
最後に,余りを右から左に向かって読みます。これが16進数に変換したときの値となります。
よって,10進数で1000は16進数で表すと3E8となります。


16進数の計算


16進数の足し算
10進数と同じように足し算を行います。その後,16以上は16進数に変換してからまた足し算します。これを,0~Fだけになるまで行います。
実際に計算してみましょう。
まずは,小学校で習った筆算のように書きます。
次に,16進数のうち,A~Fは10進数の10~15に変換します。
次に,10進数の要領で普通に計算します。
ここで,16進数は0~9とA~Fの16個の文字しか扱わないので,16以上の数値は16進数で表しましょう。
簡単に言えば,16以上の数値は16を引いて,次の位に1を追加すればOKです。
これでまた足し算します。
後は,「16以上の値が出た時は16進数の値に変える→計算する」を繰り返して,0~9とA~Fだけになるようにします。
よって,16進数で3Dと4Cを加えた値は89となります。


上で示した計算方法が面倒な場合は,10進数に変換してから計算するのがおすすめです。ただ,2進数と違って計算量が多くなるので結構大変です。
16進数:3D→10進数:48+13=61
16進数:4C→10進数:64+12=76
この値を足し合わせます。61+76=137
最後に,137を16進数に変換します。
※( )は余りを表します。
137→8(9)→0(8)
よって,89となります。

16進数の引き算
16進数の引き算は2進数よりはやりやすいですが,やはり10進数と比べるとやや違和感があります。
実際に計算してみましょう。
まずは,小学校で習った筆算のように書きます。
次に,16進数のうち,A~Fは10進数の10~15に変換します。
次に,10進数の要領で普通に計算します…が,結果がマイナスとなる場合は,次の位に「-1」を書き,もとの引かれる数に16を足します。
この計算では,2-Fはマイナスとなるため,2に16を足して18とし,代わりに2-Fの次の位に-1を書きます。
1-Aも同様にマイナスとなるため,1に16を足して17とし,代わりに1-Aの次の位に-1を書きます。
これで引き算します。-1の部分も忘れないようにしましょう。
最後に,10以上の数値がある場合は16進数に変換します。
よって,16進数で112からAFを引いた値は63となります。


上で示した計算方法が面倒な場合は,10進数に変換してから計算するのがおすすめです。ただ,やはり16進数だと計算量が多くなるので結構大変です。
16進数:112→10進数:256+16+2=274
16進数:AF→10進数:160+15=175
引き算をします。274-175=99
最後に,99を16進数に変換します。
※( )は余りを表します。
99→6(3)→0(6)
よって,63となります。

bit・byte・bps(重要度:★★★★★)
bit(ビット)とbyte(バイト)


bit(ビット)は,コンピュータで扱うデータの最小単位であり,1bitは2進数の1桁分に相当します。
つまり,1bitで,0と1の2種類のデータを扱うことができるようになります。
2bitであれば,00・01・10・11の合計4種類を,3bitであれば,000・001・010・011・100・101・110・111の合計8種類のデータを扱えるようになります。
ここで気付いた方もいると思いますが,Nbitで,2Nの情報量を扱える(重要!)ということになります。
なぜデータ量をbitで表現するのかというと,コンピュータは2進数(0と1の組み合わせ)で情報を処理しているからです。そのため,10個の情報であれば4bit,20個の情報であれば5bit必要ということになります。
例えば,「あ・い・う・え・お」の5種類の文字をコンピュータで処理する際,コンピュータは文字そのものでは処理できないため,それぞれの文字を0と1の組み合わせで表現します。
例)あ:000,い:001,う:010,え:011,お:100
そうすると,2bitでは1文字分表現できないため,この場合は3bit必要ということになり,3bit分の情報量があるということになります。


なお,8bitを1byte(バイト)とし,現在のデータ量ではこのbyteが単位として用いられています。(単位ではBと表記されます)
例)USBメモリなら4GB~,HDDなら1TBなど
実際にbitを使った問題を解いてみましょう。
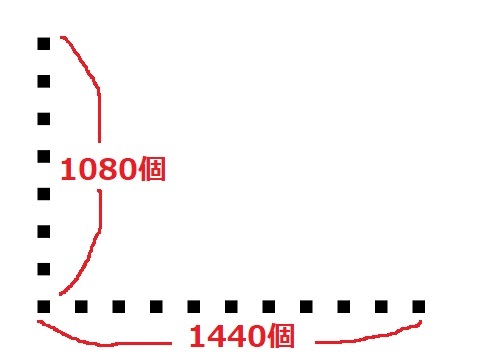
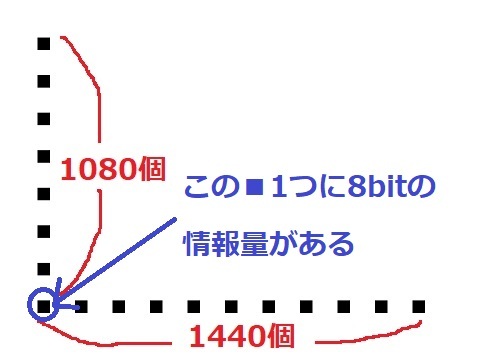
pixel(ピクセル)ということばが出てきましたが,これは画像の1つの点(=画素)のことです。
つまり,1440×1080pixelの画像というのは,横1440個,縦1080個の点の集合体と考えてください。
↑画像は点(画素)の集まり(集合体)!
そして,256色で表現ということは,1つの点,つまり1×1pixelの中に256通りの情報量があるということになります。
これはbitで表すと8bit(28=256)となるため,1つの点に8bitの情報量があるということになります。
8bit=1byteなので,この画像自体のデータ量は
1080×1440×1byte=1555200byte$\approx $1.56MBとなります。
bps(ビーピーエス)


スマホが普及した時代,一般の人でもbpsという単語は聞いたことがあるかもしれません。
これはbit per second(bit/s)の略で通信速度を表します。
例えば,1bpsなら,1秒間に1bitの情報を伝えることができるということになります。
私の使っているネット環境での通信速度は約35Mbpsで,これは1秒間に約35Mbit$\approx $4.4MBのデータを転送できることになります。
この速度なら,YoutubeのフルHD動画(約3Mbpsの通信速度が必要)でもまず不自由なく視聴できます。
逆に,スマホの通信制限(一定以上のデータ容量を使用すると自動的に低速回線となる)だと,通常128kbpsにまで速度が落とされます。
この通信制限を経験した方も多いと思いますが,こうなると動画はもちろんのこと,画像が多いwebサイトも読み込みが遅く,快適には閲覧できなくなってしまいます。
話がそれてしまいましたが,このbpsを使った問題が出るかもしれませんので,意味を覚えておきましょう。(幸いにもまだ臨床検査技師の国家試験には出題されていませんが……)


実際にbpsを使った問題を解いてみましょう。
まずは画像のデータサイズを求めましょう。
1pixelが256色なので,8bit/pixel。
これが1440×1080個あるので,画像のデータサイズは
1440×1080×8=12441600bit$\approx $12.44Mbit
後は,この式にそれぞれの値を代入します。
D:1枚当たりの画像のデータサイズ[bit]
N:画像の枚数
T:時間[s]
よって,
となります。


練習問題

問1 二進法で11と11を加えた値はどれか。(第52回臨床検査技師国家試験am85)
1.100
2.110
3.111
4.1000
5.1001
- 解答を見る
解答:2
2進数の足し算の方法を知っていればなんなく解けるはずです。よって,答えは110となります。
【別解】 10進数変換法
10進数に戻してから計算する方法でも簡単に計算できます。
11=2+1=3(10)
3+3=6(10)
6→3(0)→1(1)→0(1)
∴11+11=110
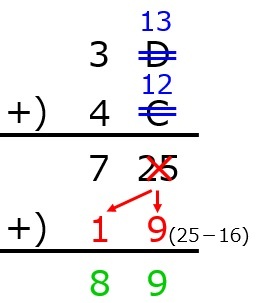
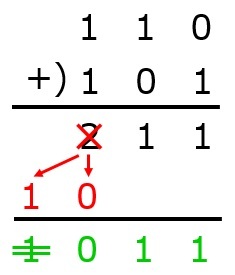
問2 二進法で110から11を引いた値はどれか。(第61回臨床検査技師国家試験pm98)
1.1
2.10
3.11
4.100
5.101
- 解答を見る
解答:3
2進数の引き算の方法を知っていれば……というが,10進数変換法のほうが簡単だったり(笑)
まずは引く数11の補数を求める。
011→100(11の補数)
次に,これに1を加える。100+1=101
最後に,引かれる数110と補数+1(101)を足し合わせて,1番上の位の1を消すと答えが出ます。よって,答えは11となります。
【別解】 10進数変換法
10進数に戻してから計算する方法のほうが簡単です。
110=4+2+0=6(10)
11=2+1=3(10)
6-3=3
3→1(1)→0(1)
∴110-11=11
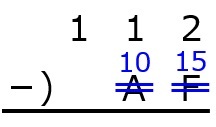
問3 16進数の減算,C8-4Aの結果を16進数で表したのはどれか。(第31回臨床工学技士国家試験am61)
1.78
2.7E
3.87
4.88
5.8E
- 解答を見る
解答:2
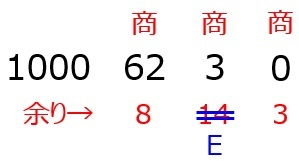
16進数の引き算の方法を知っていれば簡単です。16進数の計算では,最初にA~Fを10進数の値に変えておきましょう。
そのうえで,まず8-Aに注目すると,これはマイナスになるので,8に16を足して,代わりに次の位に-1を書きます。
後は,10進数と同じ要領で計算し,最後に10~15をA~Fに変換すればOKです。
よって,答えは7Eとなります。
【別解】 10進数変換法
10進数に戻してから計算する方法です。
C8=16×12+8=200(10)
4A=16×4+10=74(10)
200-74=126
126→7(14=E)→0(7)
∴C8-4A=7E
問4 2つの16進数A8と2Bの和を2進数で表したのはどれか。(第32回臨床工学技士国家試験am60)
1.11000011
2.11001001
3.11001010
4.11010011
5.11011001
- 解答を見る
解答:4
16進数の計算結果を16進数で表さない,つまり変換が強制的に必要な場合は,16進数を10進数に変換する計算方法を用いましょう。
(16進数での計算をしたところでまた変換が必要になってくるので)
A8=16×10+8=168(10)
2B=16×2+11=43(10)
168+43=211
計算後は,10進数を2進数に変換してあげればOKです。
211→105(1)→52(1)→26(0)→13(0)→6(1)→3(0)→1(1)→0(1)
よって,答えは11010011となります。
問5 3原色を組み合わせて画素の表示を行うディスプレーで,それぞれの色が4ビットの階調で表されるとき,画素の表現できる色の数はどれか。(第52回臨床検査技師国家試験am87)
1.12
2.64
3.256
4.1,024
5.4,096
- 解答を見る
解答:5
1色当たりの色のパターンは4bit=24=16パターンとなります。
3原色で画素を表すため,画素の色の全パターンは1色目の色のパターン数×2色目の色のパターン数×3色目の色のパターン数で表されます。よって,16×16×16=4096通りとなります。
問6 情報をコード化するとき,10ビットで表現できるコードの種類はどれか。(第56回臨床検査技師国家試験am98)
1.64
2.128
3.512
4.1,024
5.4,096
- 解答を見る
解答:4
Nbitで2Nの情報量となります。
よって,10bitでは210=1024種類となります。
問7 2バイトで表すことができる情報の個数として正しいのはどれか。(第57回臨床検査技師国家試験am98)
1.24
2.28
3.216
4.232
5.264
- 解答を見る
解答:3
1byte=8bitなので,2byte=16bit。
Nbitで2Nの情報量であるため,16bitは216となります。
問8 8bitのAD変換器で0~2.5V電圧を変換するとき,電圧の分解能に最も近いのはどれか。(第64回臨床検査技師国家試験am98)
1.1mV
2.5mV
3.10mV
4.16mV
5.20mV
- 解答を見る
解答:3
近年の国家試験の傾向なのかどうかはわかりませんが,単純な計算では答えが出せなくなっています(いわゆる難化)。ただ,ぱっと見はわからなくても,bitをきちんと理解していれば答えは出せます。まず,答えが全てmV表記であることから,問題文の電圧も0~2500mVと考えます。ここで,段階が5のときを考えてみましょう。
段階が5であれば,上のように500mV刻みで表せます。すなわち,電圧は0~2500の間で500mVずつ変換することができます。
(0~500は0mV,501~1000は500mV,1001~1500は1000mV的な感じで変換できるということ)
このときの500mVが分解能になります。
なお,計算式としては,最大値(2500mV)÷段階(5)=分解能(500mV)となります。では,今回の問題で考えてみましょう。8bitと問題文に表記されていますが,これは段階を表しています。8bit=28=256であるため,このA/D変換器は256段階で表せるということになります。(そもそもbitは情報量を表すため,256個の情報量を使って変換すると考えるとわかりやすい)
後は,分解能を求めるだけです。これは,最大値を段階で割ればOKなので,2500÷256=9.765625$\approx $9.8mVとなります。よって,これに最も近い10mVが正解となります。
問9 画素数が800×1000のモノクロ画像を128段階の濃度で表示するために必要な最小データ量[Mbyte]に最も近いのはどれか。(第30回臨床工学技士国家試験am62)
1.0.7
2.1.2
3.2.1
4.2.4
5.12.8
- 解答を見る
解答:1
まずは1pixel(1画素)のbitを求めましょう。
今回の問題では,1pixelが128段階の濃度で表示ということなので,情報量としては128=27=7bitとなります。
1pixelあたりのbit数が分かれば,後は画像の大きさを掛けるだけです。
800×1000×7=5600000=5.6×106bit=5.6Mbit
最後に,bitをbyteに変換しましょう。
よって,5.6Mbit÷8=0.7Mbyteとなります。
問10 1画面100kbitで構成されるディジタル画像を伝送したい。通信回路の伝送速度が9Mbpsであるとき,1秒間に伝送できる画像の最大数はどれか。ただし,伝送時に圧縮符号化等の処理は行わず,画像構成データ以外のデータは無視する。(第28回臨床工学技士国家試験am60)
1.1
2.9
3.10
4.90
5.100
- 解答を見る
解答:4
1画面が100kbitということであるため,要は画像1枚のデータサイズが100kbit=0.1Mbitということです。
今回は画像数を求めればいいため,$V=\frac{DN}{T}$の式を使うと,$$N=\frac{VT}{D}=\frac{9M\times 1}{0.1M}=90$$となります。
問11 各ピクセルの濃度が210=1024階調,1フレームの画像の大きさが4000×2000ピクセル,1秒間に50フレームのグレースケール動画像を,伝送速度40Mbpsの伝送路で滞留なく伝送したい。データ量は少なくとも何分の1に圧縮しなければならないか。(第32回臨床工学技士国家試験am61)
1.$\frac{1}{10}$
2.$\frac{1}{50}$
3.$\frac{1}{100}$
4.$\frac{1}{500}$
5.$\frac{1}{1000}$
- 解答を見る
解答:3
まずは1秒当たりのbit数を求めましょう。
1pixel(1画素)のbitは,1pixelが210段階の濃度で表示なので,情報量としては10bitとなります。
1pixelあたりのbit数が分かれば,後は画像の大きさを掛ければ画像1フレーム分のbit数になります。
4000×2000×10=8×107bit=80Mbit
このフレームが1秒間に50フレームあるため,1秒当たりのbit数は
80Mbit×50=4000Mbit。
これを40Mbps=40Mbit/sで送ろうとすると,T=4000/40=100sとなり,1秒分が100秒かかってしまう計算となるため,滞留なく伝送できません。今回の問題では,「滞留なく伝送」することが目的なので,1秒間の動画を最大でも1秒で伝送できるように圧縮する必要があります。
よって,4000Mbitを40Mbit($\frac{1}{100}$)にまで圧縮する必要があり,答えは$\frac{1}{100}$となります。






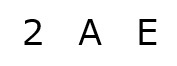

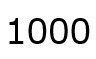

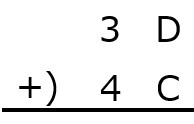
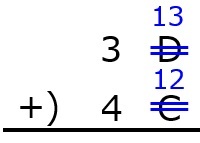
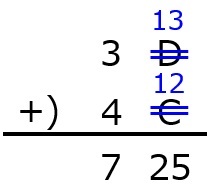
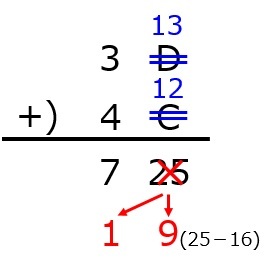
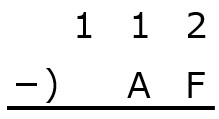
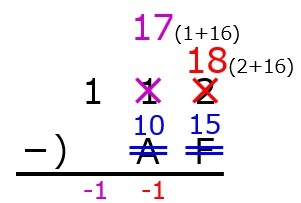
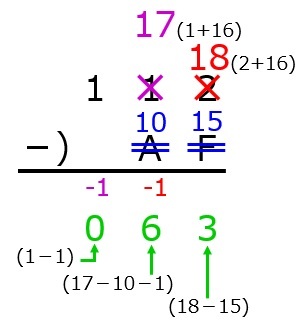


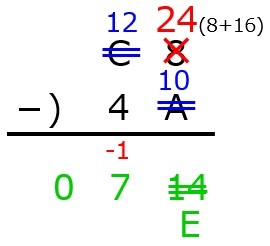



コメント