国家試験で出題される電気回路について解説します!電気回路の計算が苦手な方必見!
※スマホから閲覧している場合,数式をスクロールできます。
各見出しの重要度は,過去の臨床検査技師国家試験(第52回~最新回まで)の出題率や覚えやすさなどを考慮して主観で表記しています。国家試験を受ける学生以外の方は無視してかまいません。
オームの法則(重要度:★★★★☆)
国試ではたまに電気回路の問題が出題されます。
一見難しそうに見えますが,中学校で習うオームの法則を知っておけば楽に解くことができます。


E:起電力(電圧)[V]
I:電流[A]
R:抵抗[Ω]
※オームの法則は,直流・交流のいずれも成り立つ法則です。
この式を覚えていないと電気回路の問題は解けないので,絶対に覚えましょう!
(考え方として,電圧は必ず割られる側(分子)となり,これを求めるときだけ掛け算を使うと覚えておくといいと思います)


式だけだとわかりづらいので,実際に図を見てみましょう。
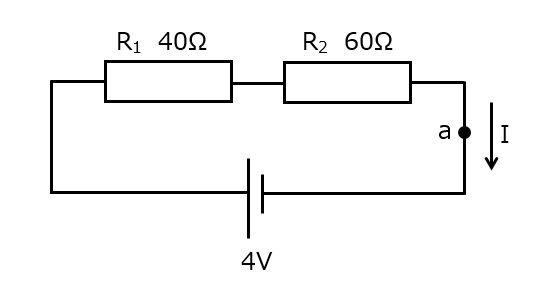
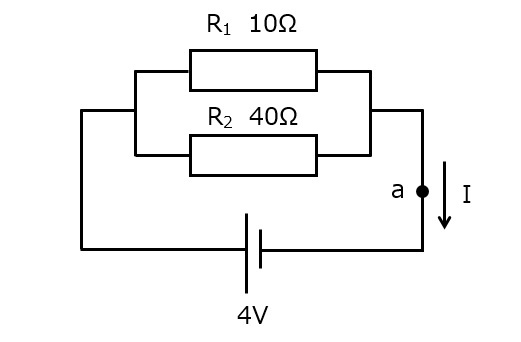
図1
図1の||が電池を,□が抵抗を示しています。
この回路では,電池の起電力(電圧)が4V,抵抗値が40Ωであるため,a点を流れる電流Iは
となります。

基本的に,オームの法則では,抵抗を1つとして考えます。次に,抵抗が2つ以上ある場合を考えていきましょう。
合成抵抗(重要度:★★★★☆)


回路に抵抗が1個しかなければ,単純にオームの法則を使うことで電圧や電流を求めることができます。
しかしながら,回路に抵抗が2つ以上あると,単純な計算では電圧や電流を求めることができません。こういう時は,抵抗を1個とみなすことで,回路全体の電圧や電流を求めることができます。
このときの抵抗値を合成抵抗と呼びます。
ここからは,実際の回路を見ながら,合成抵抗について考えていきましょう。
直列に接続された抵抗の合成抵抗
直列とは,回路に分岐がない状態です。例題2を見てみましょう。
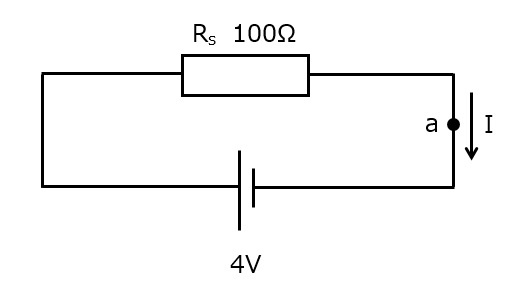
図2
図2の回路を流れる電流を求めたいのですが,抵抗が2つあるため,この状態ではオームの法則が使えません。なので,抵抗を1個にしてやる必要があります。
直列に接続された抵抗の場合は,単純に抵抗値を足し合わせればOKです。
Rs:直列の合成抵抗[Ω]
R1~Rn:各抵抗(n個)[Ω]


図2の場合は,抵抗値がそれぞれ40Ω,60Ωであるため,合成抵抗Rsは
となります。
合成抵抗を考えることで,図2は図2’と考えることができます。
図2′
したがって,a点を流れる電流Iは
となります。
並列に接続された抵抗の合成抵抗
並列とは,回路に分岐がある状態です。例題3を見てみましょう。
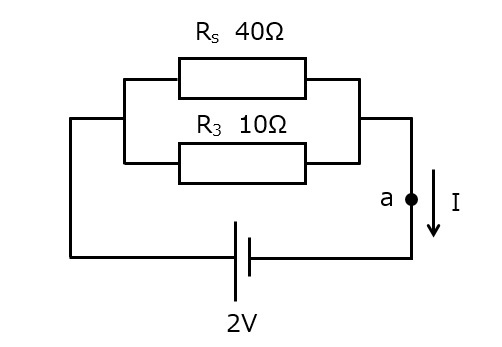
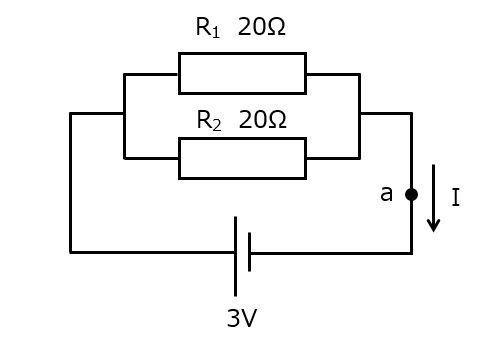
図3
図3の回路を流れる電流を求めたいのですが,抵抗が2つあるため,この状態ではオームの法則が使えません。なので,抵抗を1個にしてやる必要があります。
並列に接続された抵抗の場合は直列と違ってちと厄介で,簡単には求められません。出し方を頭に入れておく必要があります。
Rp:並列の合成抵抗[Ω]
R1~Rn:各抵抗(n個)[Ω]




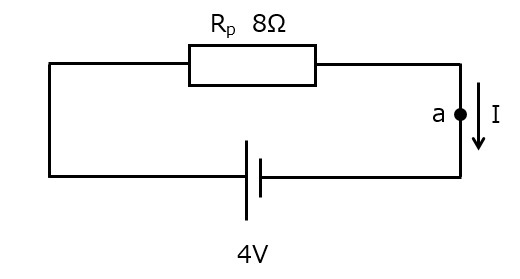
図3の場合は抵抗値がそれぞれ10Ω,40Ωであるため,回路全体の抵抗値Rpは
となります。
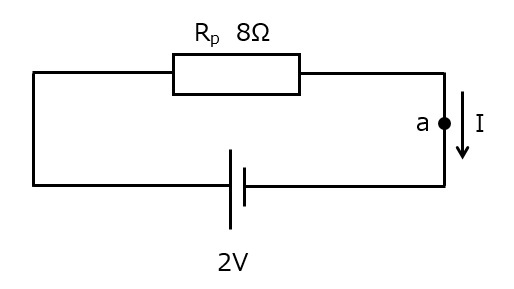
合成抵抗を考えることで,図3は図3’と考えることができます。
図3′
したがって,a点を流れる電流Iは
となります。
並列の合成抵抗を求める方法は覚えにくいですが,国家試験ではこれを知っておかないと解けない問題が出題されるため,嫌でも覚えましょう(泣)
先ほど公式を紹介しましたが,並列の抵抗が2つの場合はもっと簡単に合成抵抗を出すことができます。
$$R_p=\frac{R_1\times R_2}{R_1+R_2}$$
これを『和分の積』といいます。
図3の場合では,抵抗が2つなので,和分の積で合成抵抗を求めることもできます。
国試では基本的に抵抗2つの並列が出題されるので,これを知っておくとかなり計算が楽になります。


直列と並列の複合
ここまでは抵抗2つの場合を考えてきました。3つ以上ある場合でも,基本的には同じです。
では,実際に回路を見ていきましょう。
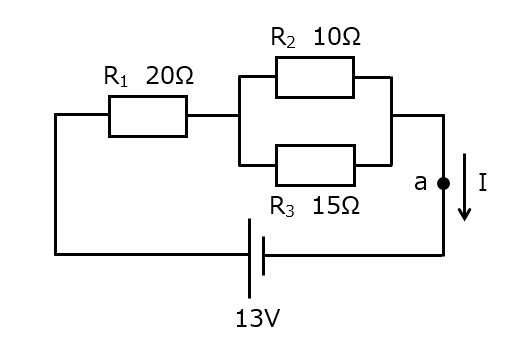
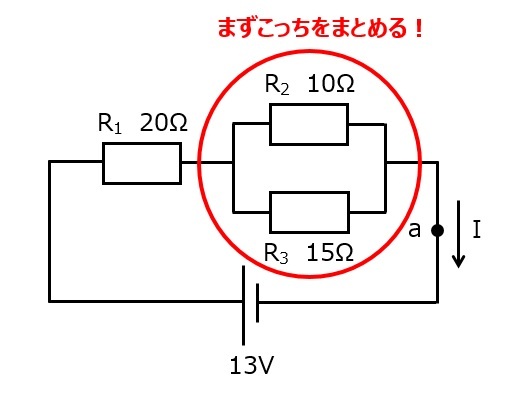
図4
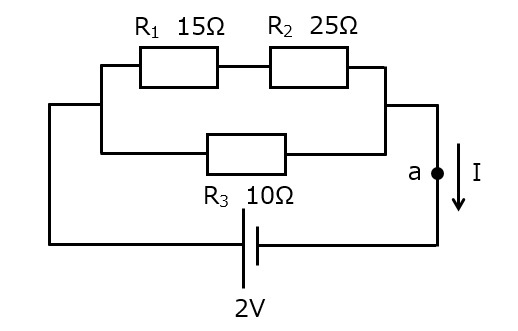
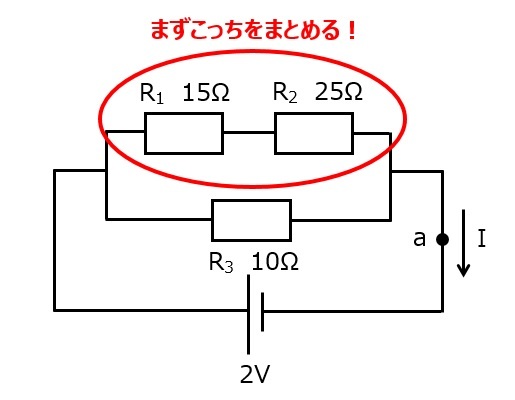
図5


ここでポイントなのは,回路を簡単にすること,つまり,回路に存在する抵抗の数を減らすことです。焦らず,少しずつ減らしていきます。
図4は,並列回路の抵抗が減らせそうなので,まず並列の合成抵抗を求めます。
並列部分の合成抵抗Rpは,和分の積を用いると
となります。
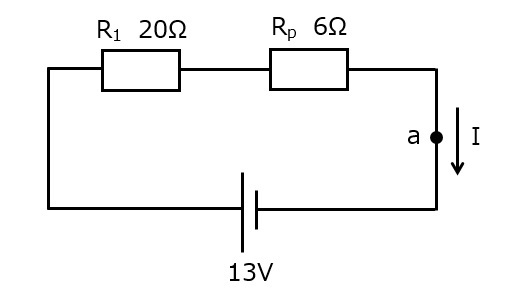
簡単にした結果を図にしてみます。(図4a)
図4a
抵抗の数を減らしたことで,抵抗2つの直列回路として見なすことができました。後は,直列の抵抗2つを足し合わせればOKです。
直列部分の合成抵抗Rsは
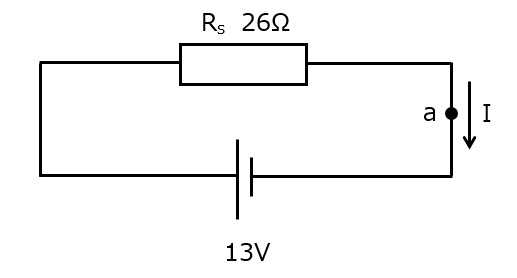
となります。(図4b)
図4b
よって,a点を流れる電流Iは
となります。
図5は,直列回路の抵抗が減らせそうなので,まず直列の合成抵抗を求めます。
直列抵抗の合成抵抗Rsは,足し合わせるだけなので,
$$R_s=15+25=40Ω$$
となります。こちらも,簡単にした結果を図にしてみます。(図5a)
図5a
抵抗の数を減らしたことで,抵抗2つの並列回路として見なすことができました。後は,並列の合成抵抗を求めます。
並列部分の合成抵抗Rpは,和分の積を用いると
となります。(図5b)
図5b
よって,a点を流れる電流Iは
となります。


直列および並列の電流・電圧分配(重要度:★★★☆☆)


これまでは,抵抗の数を1個としてオームの法則を使っていました。
ただ,実際には「この抵抗にかかる電圧or流れる電流はいくらか」といった問題も出題されます。
ここでは,複数個の抵抗が直列または並列で接続されている場合の,各抵抗にかかる電圧・流れる電流を計算する方法を説明します。
直列の場合
図があったほうが分かりやすいので,まずは,図を見てみましょう。
(先ほど直列の合成抵抗の説明で使った回路図です)
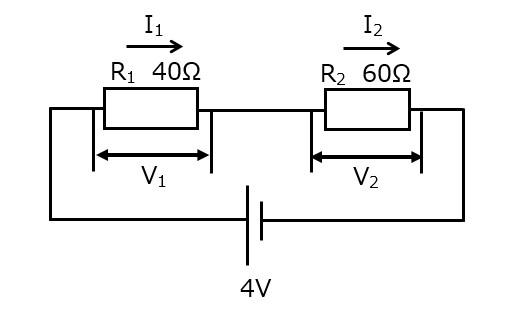
図6
図6の回路では,抵抗2つが直列に接続されています。
このそれぞれの抵抗にかかる電圧・流れる電流を考えてみます。
電流分配
直列の場合,電流は簡単で,直列部分の各抵抗を流れる電流の大きさは全て同じです。
よって,合成抵抗Rsが100Ωであることから,
となります。


電圧分配
電圧は2つの求め方があります。新しいことを覚えたくない人は,方法1のほうがいいでしょう。(楽なのは方法2ですが)
方法1 抵抗値とその部分を流れる電流からオームの法則を用いて求める
スタンダードな計算法です。
それぞれの抵抗について,オームの法則を用いて電圧を求めます。
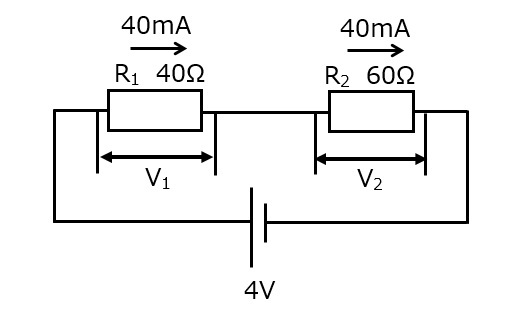
R1・R2ともに流れる電流は40mAであるため,オームの法則でそれぞれの電圧を求めます。
電流を求める必要があるので面倒ですが,オームの法則さえ覚えておけば間違いなく計算できます。
なお,起電力EはE=V1+V2=1.6+2.4=4Vとなり,計算が正しいことが確認できます。
方法2 抵抗比=電圧比であることを用いて求める
直列に接続された部分では,抵抗比=電圧比の式が成り立ちます。
実際に見たほうが早いでしょう。
抵抗値はそれぞれ40Ωと60Ωなので,抵抗比は40:60。
その抵抗にかかる電圧はそれぞれV1とV2なので,電圧比はV1:V2。
抵抗比=電圧比なので,
この回路の全体の電圧は4Vであるため,V1・V2は
となります。
抵抗の数が少なければこちらのほうが簡単です。
なお,起電力EはE=V1+V2=1.6+2.4=4Vとなり,計算が正しいことが確認できます。


並列の場合
直列同様図があったほうが分かりやすいので,まずは,図を見てみましょう。
(先ほど並列の合成抵抗の説明で使った回路図です)
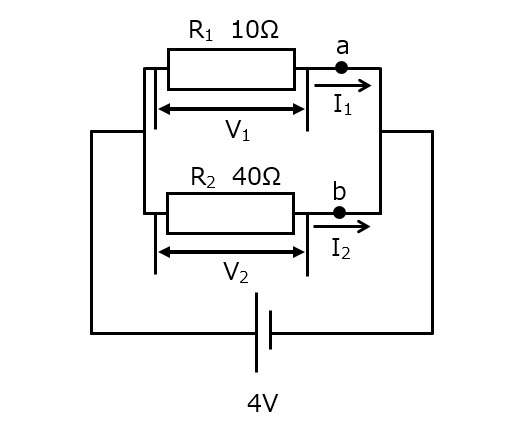
図7
図7の回路では,抵抗2つが並列に接続されています。
このそれぞれの抵抗にかかる電圧・流れる電流を考えてみます。
電圧分配
並列の場合は直列と逆で,並列部分の各抵抗にかかる電圧の大きさは全て同じとなります。
よって,
となります。


電流分配
直列と同じように,並列での電流は2つの求め方があります。こちらは直列と違って,方法1のほうが圧倒的に簡単です。なので,方法2は「こんな求め方もあるんだ~」くらいに思っておけばOKです。
方法1 抵抗値とその部分にかかる電圧からオームの法則を用いて求める
スタンダードな計算法です。
それぞれの抵抗について,オームの法則を用いて電流を求めます。
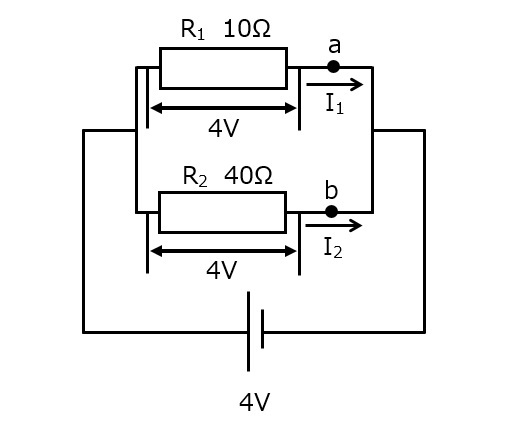
R1・R2ともにかかる電圧は4Vであるため,オームの法則でそれぞれの電流を求めます。
計算間違いさえしなければ簡単に求められます。
なお,回路全体を流れる電流は,I1+I2=500mAとなります。
方法2 抵抗の逆数の比=電流比であることを用いて求める
この方法は基本使うことはないのですが,気になる方はどうぞ。
- 詳細を見てみる
並列に接続された部分では,抵抗の逆数の比=電流比の式が成り立ちます。
実際に見たほうが早いでしょう。抵抗値はそれぞれ10Ωと40Ωなので,抵抗比は10:40。
その抵抗を流れる電流はそれぞれI1とI2なので,電流比はI1:I2。
抵抗の逆数の比=電流比なので,$$\frac{1}{R_1}:\frac{1}{R_2}=I_1:I_2$$$$\frac{1}{10}:\frac{1}{40}=I_1:I_2$$$$I_1:I_2=\frac{1}{10}:\frac{1}{40}=4:1$$次に,この回路全体を流れる電流を求めます。
並列部分の合成抵抗Rpは$$R_p=\frac{10\times 40}{10+40}=8Ω$$であるから,電流Iは,$$I=\frac{4}{8}=500\,\mathrm{mA}$$となります。よって,a点・b点を流れる電流はそれぞれ
$$I_1=500\times \frac{4}{1+4}=400\,\mathrm{mA}$$$$I_2=500\times \frac{1}{1+4}=100\,\mathrm{mA}$$となります。
合成抵抗を求めて回路全体の電流を求めなければならないうえ,「抵抗の逆数の比」というのがややこしいため,この方法を使うことはまずないと思いますが,参考程度に……。 ペンギンくん
ペンギンくん この方法って難しいね。
この方法って難しいね。 国試だと使うことはないから,覚える必要はないかな。
国試だと使うことはないから,覚える必要はないかな。 おるてぃ
おるてぃ
内部抵抗(重要度:★★☆☆☆)




内部抵抗とは,電源等の中にある抵抗のことです。
過去の国家試験では内部抵抗が存在する電池が登場する問題が1問出題されており,計算方法を知らないと苦戦します。
ただ,考え方は非常にシンプルで,起電力を持った抵抗と考えればOKです。実際に回路を見てみましょう。
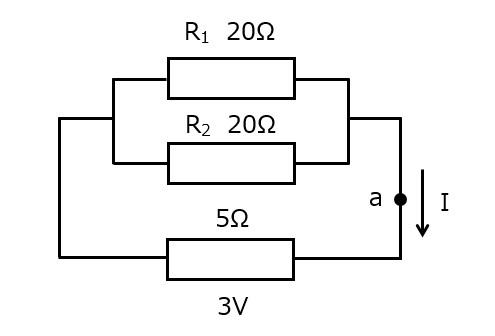
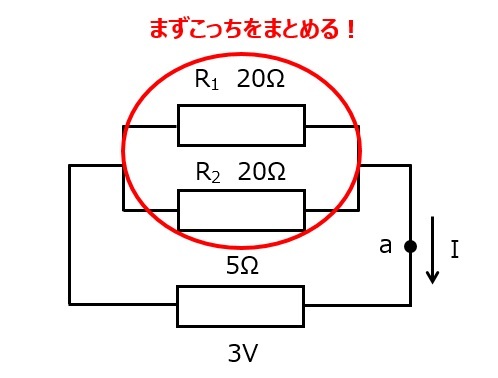
図8
図8に存在する電池には5Ωの内部抵抗が存在します。この場合は,図8aのように,電池を抵抗に変換してしまいましょう。
図8a
後は,抵抗の数を1個にして,電流を求めればOKです。
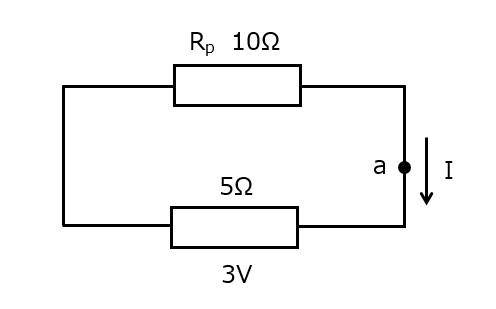
まずは,並列の合成抵抗Rpを求めます。(結果→図8b)
図8b
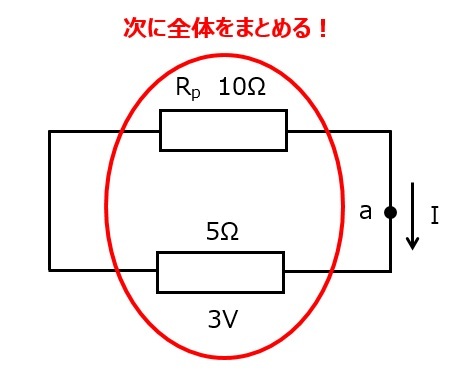
次に,直列の合成抵抗Rsを求めます。(結果→図8c)
$$R_s=10+5=15Ω$$
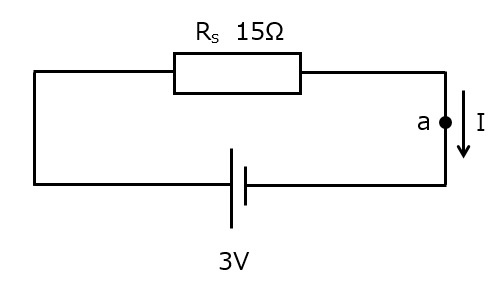
図8c
最後に,オームの法則で電流を求めると
となります。
この考え方を知らないと手も足も出ないのですが,知っておきさえすれば,後は合成抵抗とオームの法則の考え方に落とし込めるので楽に解けると思います。


練習問題

問1 100kΩの抵抗器にもう1つの抵抗器を並列に接続し,それらの合成抵抗を50kΩとしたい。接続すべき抵抗器の抵抗値[kΩ]はどれか。(第63回臨床検査技師国家試験am95)
1.0.5
2.1
3.50
4.100
5.500
- 解答を見る
解答:4
並列で抵抗が2つなので,「和分の積」を使って求めます。
新たに接続する抵抗の抵抗値をR[kΩ]とすると,$$50=\frac{100\times R}{100+R}$$$$50(100+R)=100R$$$$5000+50R=100R$$$$50R=5000 R=100$$となります。
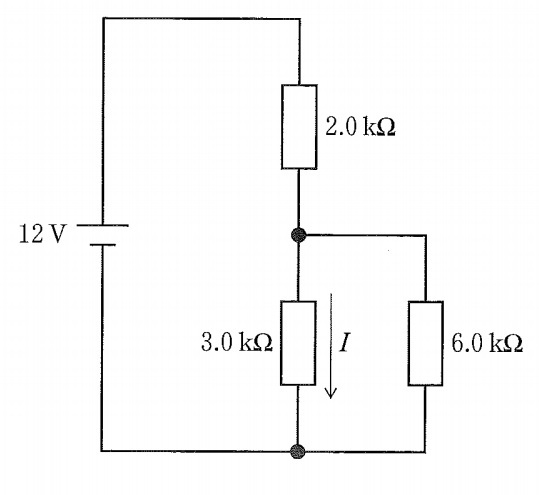
問2 図の回路で3.0kΩの抵抗を流れる電流I[mA]はどれか。(第28回臨床工学技士国家試験pm48)
1.1.0
2.1.5
3.2.0
4.3.0
5.4.8
- 解答を見る
解答:3
抵抗が3つあって厄介そうですが,「並列部分にかかる電圧」を求めれば,オームの法則で解けそうです。
よって,まずは並列部分の合成抵抗Rpを求めます。$$R_p=\frac{3\,\mathrm{k}\times 6\,\mathrm{k}}{3\,\mathrm{k}+6\,\mathrm{k}}=2\,\mathrm{k}Ω$$次に,並列部分(合成抵抗にした部分)にかかる電圧を求めます。
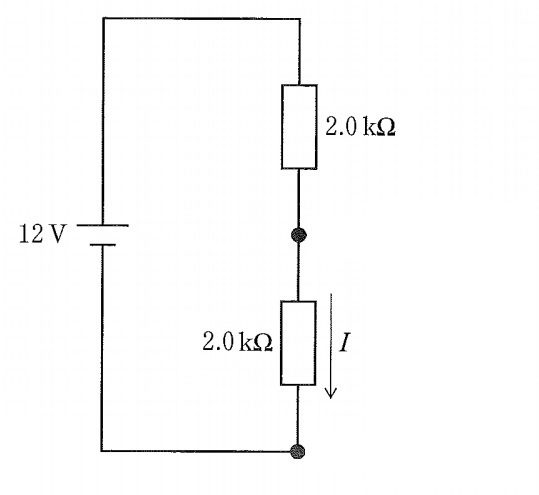
これは,抵抗比=電圧比なので,上の抵抗にかかる電圧をV1,下の抵抗(合成抵抗)にかかる電圧をV2とすると$$V_1:V_2=2\,\mathrm{k}:2\,\mathrm{k}=1:1$$よって,
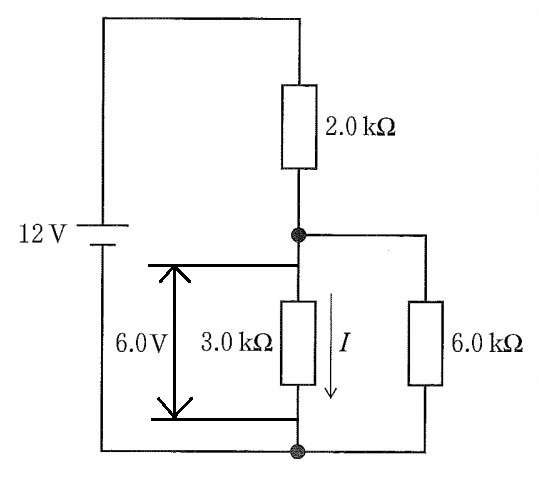
$$V_2=12\times \frac{1}{1+1}=6\,\mathrm{V}$$この結果を図にするとこうなります。
後は,オームの法則を使って電流を求めればいいので
$$I=\frac{6}{3\,\mathrm{k}}=2\times 10^{-3}=2\,\mathrm{mA}$$となります。
計算自体は簡単ですが,k(キロ)に注意です!
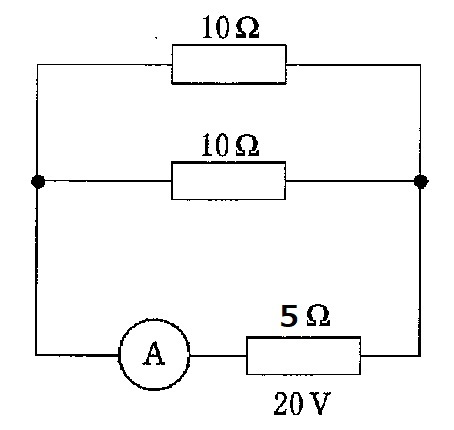
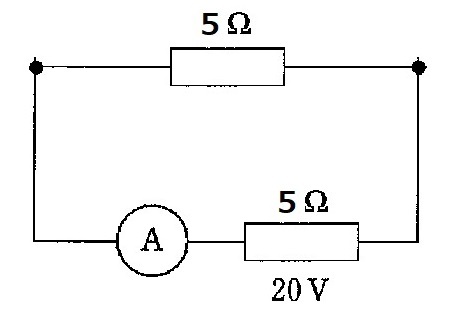
問3 抵抗2つを並列につないだ直流回路を図に示す。電流計が示す電流値[A]はどれか。ただし,電池の内部抵抗を5Ωとする。(第57回臨床検査技師国家試験pm95)
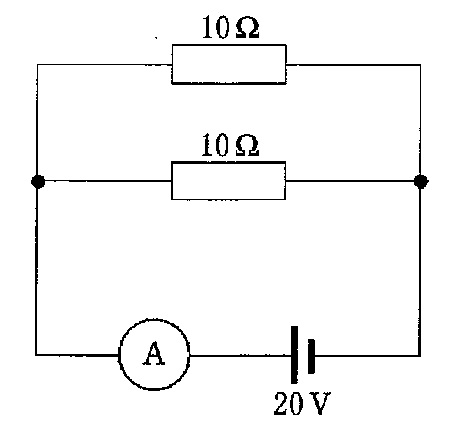
出典:厚生労働省ホームページ 第57回臨床検査技師国家試験問題および正答について 午後(https://www.mhlw.go.jp/topics/2011/04/dl/tp_siken_57_rinken_03.pdf)
1.0.8
2.1.3
3.2.0
4.4.0
5.8.0
- 解答を見る
解答:3
内部抵抗があるため,簡単には求められません。並列と直列の合成抵抗の求め方を使う必要があります。
内部抵抗がある際には,まずその部分を抵抗に置き換えることから始めます。後は,合成抵抗を求めるだけです。まずは,並列部分の合成抵抗Rpを求めます。
$$R_p=\frac{10\times 10}{10+10}=5Ω$$
これを図にするとこうなります。
次に,直列の合成抵抗Rsを求めます。$R_s=5+5=10Ω$
全体の抵抗の合成抵抗を求められたので,後はオームの法則に代入するだけです。したがって,$$I=\frac{20}{10}=2.0\,\mathrm{A}$$となります。
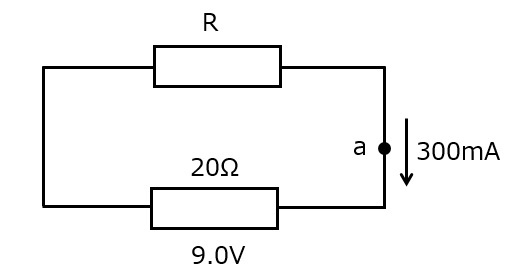
問4 開放電圧が9.0V,内部抵抗が20Ωの電池に負荷抵抗を接続すると300mAの電流が流れた。負荷抵抗の大きさ[Ω]はどれか。(第29回臨床工学技士国家試験pm50)
1.2.0
2.6.0
3.10
4.20
5.30
- 解答を見る
解答:3
開放電圧やら負荷抵抗やら聞きなれない言葉が並んでいますが,簡単に言い直すと,「起電力9.0V,内部抵抗20Ωの電池に何Ωの抵抗をつなぐと回路に300mA流れますか?」ということです。図で表すとこんな感じ。内部抵抗の扱い方とオームの法則さえ覚えておけば何ら問題なく解けます。
負荷抵抗の大きさをR[Ω]とすると,$$9.0=300\,\mathrm{m}\times (R+20)$$$$300\,\mathrm{m}R=9-6000\,\mathrm{m}=9-6=3$$$$R=\frac{3}{300\,\mathrm{m}}=\frac{3}{0.3}=10Ω$$となります。m(ミリ)の取り扱いには注意しましょう。
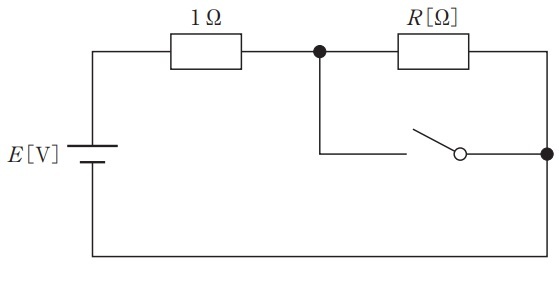
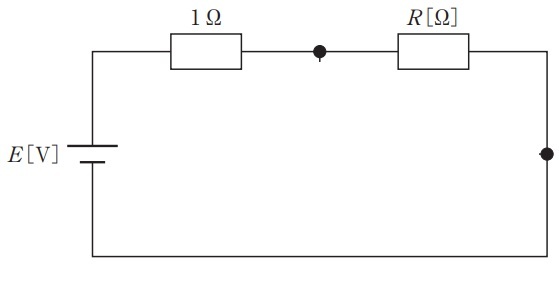
問5 図の回路において,スイッチを閉じると,閉じる前と比べて1Ωの抵抗に流れる電流[A]が2倍となった。この時の抵抗R[Ω]はどれか。(第31回臨床工学技士国家試験am49)
1.0.2
2.0.5
3.1
4.2
5.5
- 解答を見る
解答:3
回路の一部が短絡(ショート)している回路図です。短絡回路は説明していないのですが,0Ωの抵抗がつながっていると考えるとわかりやすいです。
まず,スイッチを閉じる前(開いた状態)を考えます。図を示すとこんな感じです。この時は,単に抵抗2つの直列回路ですので,合成抵抗Rsは$R_s=1+R Ω$となり,スイッチを開いた状態の回路を流れる電流Ioは
$$I_o=\frac{E}{1+R} (1)$$となります。
次に,スイッチが閉じた後を考えます。図を示すとこんな感じです。なお,スイッチ側は,考えやすいように,0Ωの抵抗を書いておきます。
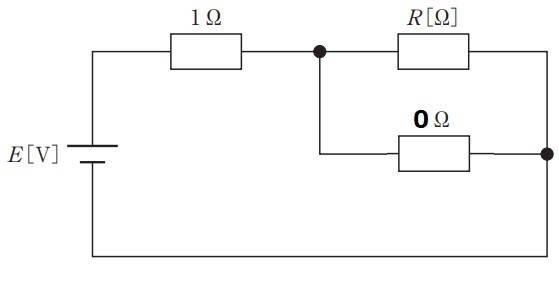 ここから合成抵抗を考えていきます。まずは,並列の合成抵抗Rpを求めます。$$R_p=\frac{R\times 0}{R+0}=0Ω$$
ここから合成抵抗を考えていきます。まずは,並列の合成抵抗Rpを求めます。$$R_p=\frac{R\times 0}{R+0}=0Ω$$なんと,並列部分の合成抵抗が0Ωとなりました!これが短絡回路の特徴です。
これより,回路全体の合成抵抗は$1+0=1Ω$となり,スイッチを閉じた状態の回路を流れる電流Icは$$I_c=\frac{E}{1}=E (2)$$となります。
問題文には,「スイッチを閉じた後の電流が閉じる前の電流の2倍」と記されているため,これを満たす方程式をたてると$$I_c=2I_o$$となります。後は,先ほどの(1)・(2)を代入するだけです。よって,$$E=2\times \frac{E}{1+R}$$$$1=\frac{2}{1+R}$$$$1+R=2 R=1Ω$$となります。
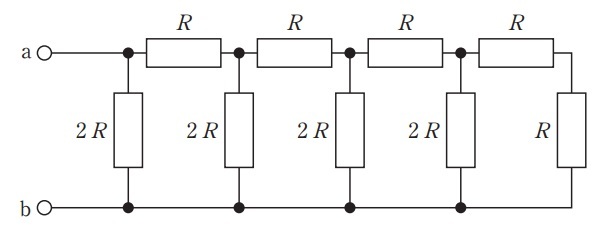
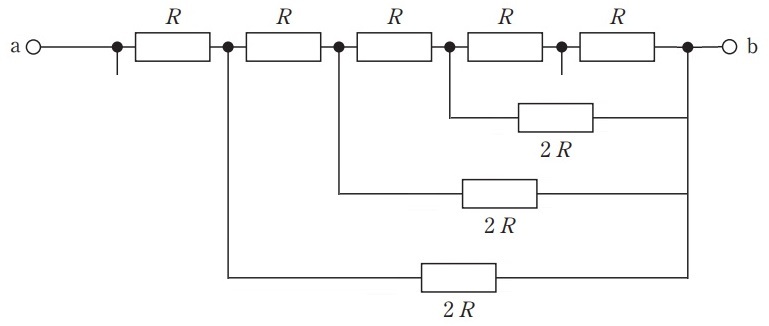
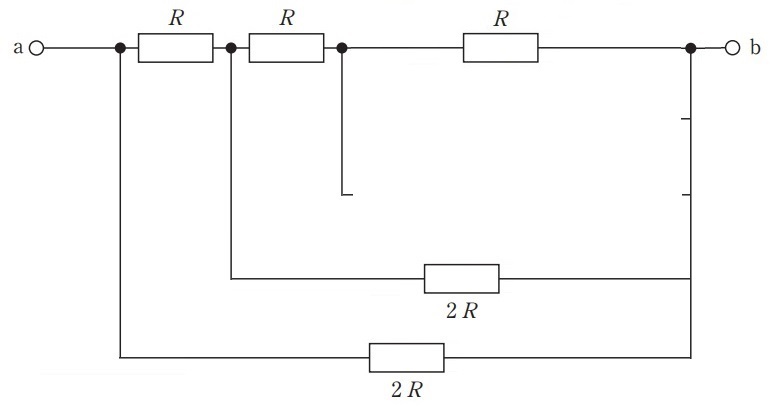
問6 図の回路で端子ab間の合成抵抗はどれか。(第29回臨床工学技士国家試験pm49)
1.$\frac{1}{3}$R
2.$\frac{1}{2}$R
3.R
4.2R
5.3R
- 解答を見る
解答:3
抵抗が多すぎて気持ち悪いですね……。人によっては解く気も失せそうですが,これも並列と直列の合成抵抗の求め方を知っていれば合成抵抗は出せます。それ以上に,この回路をわかりやすく書き直すほうが重要です。(上の画像だとわかりにくいので)
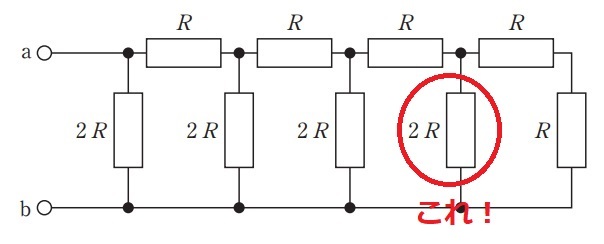
まずは直列部分のみを書き出します。次に並列部分の抵抗を1つずつ追加していきます。まずは,一番右の抵抗です。
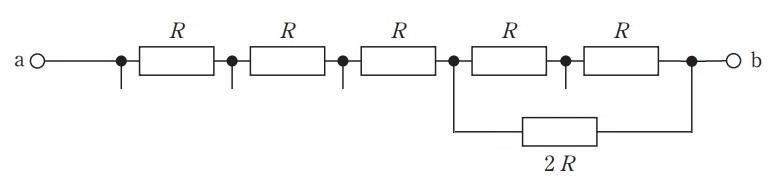
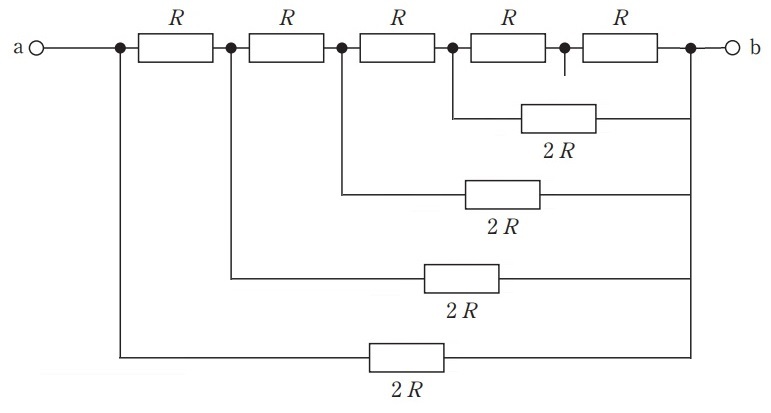
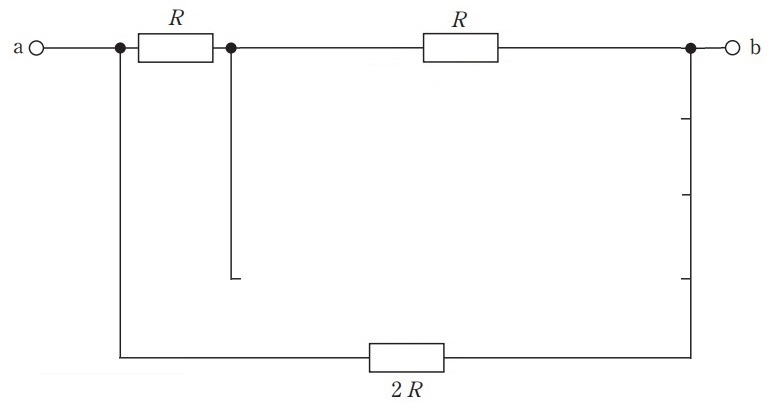
この抵抗は,直列の右2つの抵抗に並列につながっているので,わかりやすく書き直すとこうなります。
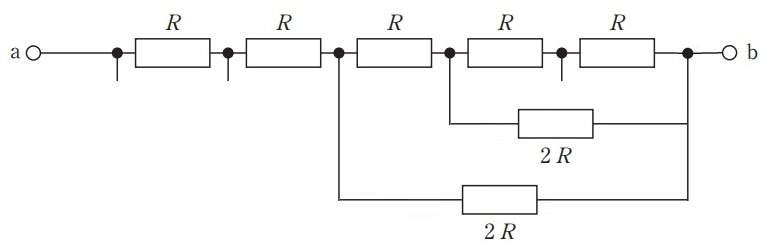
同じように,並列部分の抵抗を1つずつ追加していきます。
↓
↓
これさえ書ければ,後は少しずつ抵抗を減らしていけば簡単に合成抵抗を求めることができます。
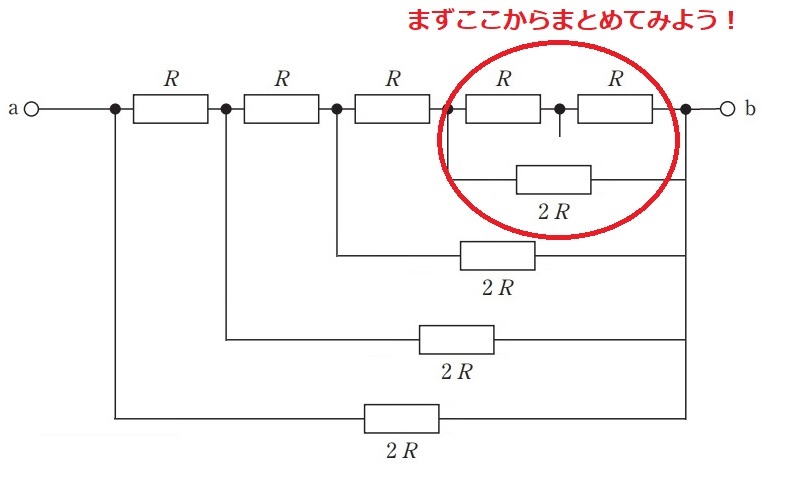
最初に求められそうなのは右側の抵抗部分ですので,ここから合成抵抗を求めてみましょう。
$$R_s=R+R=2R$$$$R_p=\frac{2R\times 2R}{2R+2R}=\frac{4R^2}{4R}=R$$まとめた結果,下の図のようになります。
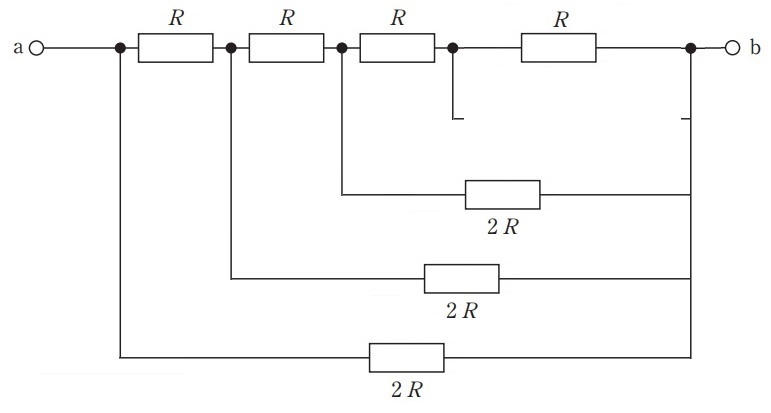
残りの部分も同様に直列→並列で合成抵抗を求めていくと,最終的にRとなります。
↓
↓
たくさんの抵抗があるときは,自分にとってわかりやすく回路を書き直すのがコツです。(回路を書き間違えないように注意!)







コメント